
ij�����м���ԭ��69ǧ�ˣ�����ԭ��52ǧ�ˣ��ּƻ���������ԭ������A��B�����ͺŵIJ�Ʒ��80������֪ÿ��A�ͺŲ�Ʒ��Ҫ����ԭ��0.6ǧ�ˣ�����ԭ��0.9ǧ�ˣ�ÿ��B�ͺŲ�Ʒ��Ҫ����ԭ��1.1ǧ�ˣ�����ԭ��0.4ǧ�ˣ������������⣺
��1���ù������ļ�������������
��2����������Ʒȫ���۳��������£���1��A�ͺŲ�Ʒ����35Ԫ��1��B�ͺŲ�Ʒ����25Ԫ����1�������ַ������������������Ƕ��٣�
��3���ڣ�2���������£��������������������25%ȫ�������ٴι����ס�������ԭ�ϣ�Ҫ��ÿ��ԭ�����ٹ���4ǧ�ˣ��ҹ���ÿ��ԭ�ϵ�������Ϊ������������ԭ��ÿǧ��40Ԫ������ԭ��ÿǧ��60Ԫ����ֱ��д������ס�������ԭ��֮�����ķ�����
�⣺��1��������A�ͺŲ�Ʒx����������B�ͺŲ�Ʒ��80��x�����������⣬��
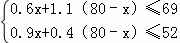 ��
��
��ã�38��x��40��
��x������
��x=38��39��40��
����3�ֹ�����
����1������A�ͺŲ�Ʒ38��������B�ͺŲ�Ʒ42����
����2������A�ͺŲ�Ʒ39��������B�ͺŲ�Ʒ41����
����3������A�ͺŲ�Ʒ40��������B�ͺŲ�Ʒ40����
��2������������ΪWԪ�������⣬��
W=35x+25��80��x����
w=10x+2000��
��k=10��0��
��W��x�����������
�൱x=40ʱ��W���=2400Ԫ��
������A�ͺŲ�Ʒ40����B�ͺŲ�Ʒ40��ʱ��������������Ϊ2400Ԫ��
��3���蹺�����ԭ��mǧ�ˣ���������ԭ��nǧ�ˣ������⣬��
40m+60n=2400
2m+3n=120��
��m+nҪ���
��nҪ��С��
��m��4��n��4��
��n=4��
��m=9��
�߹������ԭ��9ǧ�ˣ�����ԭ��4ǧ�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
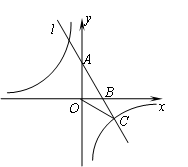
��ͼ������B��2��0����ֱ��l��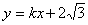 ��y���ڵ�A���뷴��������
��y���ڵ�A���뷴��������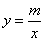 ��ͼ���ڵ�C��3��n����
��ͼ���ڵ�C��3��n����
��1�����������Ľ���ʽ��
��2������OBC�Ƶ�O��ʱ�뷽����ת���ǣ���Ϊ��ǣ����õ���OB��C������OC����ABʱ�����߶�OCɨ���������
 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��һ�������Ŀڴ�����3����ȫ��ͬ��С�����Ƿֱ���Ϊ1��2��3�������ȡ��һ��С��Ȼ��Żأ��������ȡ��һ��С��������ȡ��С��ı�ŵĺ���3�ı����ĸ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
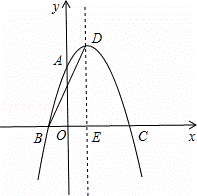
��ͼ��������y=ax2+2x+c������A��0��3����B����1��0���������������⣺
��1���������ߵĽ���ʽ��
��2�������ߵĶ���Ϊ��D���Գ�����x�ύ�ڵ�E������BD����BD�ij���
ע��������y=ax2+bx+c��a��0���Ķ��������ǣ���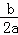 ��
��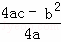 ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ijУ�涨��ѧ������ѧѧ���ۺϳɼ�����ƽʱ�����к���ĩ����ɼ���3��3��4�ı����������ã���ijͬѧ��ѧ����ѧ��ƽʱ�����к���ĩ�ɼ��ֱ���90�֣�90�ֺ�85�֣�������ѧ����ѧѧ���ۺϳɼ����� ���֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���м�����ȷ���ǣ� ��
A��a2��a4��a6 B��2a��3b��5ab C��(a2)3��a6 D��a6��a3��a2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
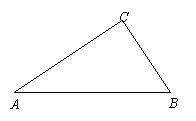
��ͼ����ֱ֪��������ABC����C=90�㣮
��1������ֱ�ߺ�Բ�����������ͼ������������ABC������CE��
������ACD��ʹ�����ACE����ֱ��AC�Գ�.
��2����֤����1���е��ı���ADCE�����Σ�
 ��3����֤��BC=E.D
��3����֤��BC=E.D
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com