

分析 (1)根据切线的性质得出O1C⊥AC,由sinA=$\frac{{O}_{1}C}{{O}_{1}A}$=$\frac{1}{2}$,得出∠OAD=30°,从而求得直线AC的斜率为$\frac{\sqrt{3}}{3}$,设直线AC的解析式为y=$\frac{\sqrt{3}}{3}$x+b,利用待定系数法求得b,即可求得D的坐标.
(2)先证得△O2AD是等边三角形,再证明△PAE≌△NFE,得出PE=NE,△PNE是等边三角形,PE=EN=PN,即可得出答案;
(3)首先得出∠R=∠Q,根据等角对等边得出RH=QH,根据等腰三角形三线合一的性质得出HN⊥RQ,进而根据直角三角形斜边中线等于斜边的一半的性质,即可证得MN=MG.
解答  (1)解:连接O1C,
(1)解:连接O1C,
∵AC与⊙O1相切于点C,
∵O1C⊥AC,
∵A(-1,0)、B(2,0),以OB为直径作⊙O1,
∴O1A=2,O1C=1,
∴sinA=$\frac{{O}_{1}C}{{O}_{1}A}$=$\frac{1}{2}$,
∴∠OAD=30°,
∴$\frac{OD}{OA}$=tan30°=$\frac{\sqrt{3}}{3}$,
∴设直线AC的解析式为y=$\frac{\sqrt{3}}{3}$x+b,
把A(-1,0)代入得,$\frac{\sqrt{3}}{3}$×(-1)+b=0,
解得b=$\frac{\sqrt{3}}{3}$,
∴点D的坐标为(0,$\frac{\sqrt{3}}{3}$);
(2)PF=PA+PE.
证明:∵∠OAD=30°,
∴∠ADO=60°,
∵O2A=O2D,
∴△O2AD是等边三角形,
∴∠APF=∠ADF=60°,连接EF,
在FP上截取FN=AP,连接EN,
∵O2D=2OD=$\frac{2\sqrt{3}}{3}$,
∴OF=$\frac{2\sqrt{3}}{3}$+$\frac{\sqrt{3}}{3}$=$\sqrt{3}$,
∵OE=OA=1,
∴EF=$\sqrt{O{E}^{2}+O{F}^{2}}$=2,
∵AE=2,
∴EF=AE,
∵在△PAE和△NFE中,
$\left\{\begin{array}{l}{AE=EF}\\{∠PAE=∠PFE}\\{AP=FN}\end{array}\right.$,
∴△PAE≌△NFE(SAS),
∴EN=PE,
∵DF垂直平分AE,
∴$\widehat{AF}$=$\widehat{EF}$,
∴∠EPF=∠APF=60°,
∴△PNE是等边三角形,PE=EN=PN,
∴PA+PE=PF;
(3) 当Q点运动时,MN的值不发生变化;
当Q点运动时,MN的值不发生变化;
理由:连接NH、RH、QH,
∵⊙O与⊙O1的半径相等,
∴$\widehat{GOH}$=$\widehat{G{O}_{1}H}$,
∴∠R=∠Q,
∴RH=QH,
∵N是QR的中点,
∴HN⊥RQ,
在RT△NHG中,GM=HM,
∴MN=$\frac{1}{2}$GH=GM,
即MN=MG.
∵$\frac{1}{2}$GH=cos60°×1=$\frac{\sqrt{3}}{2}$,
∴MN=$\frac{\sqrt{3}}{2}$.
点评 此题主要考查了切线的性质、解直角三角形、待定系数法求解析式、勾股定理的应用、等边三角形的判定与性质以及圆周角定理等知识,熟练掌握和正确应用性质定理是解题关键.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
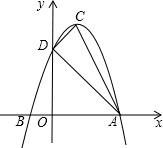 如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),B两点,交y轴于点D.
如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),B两点,交y轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com