
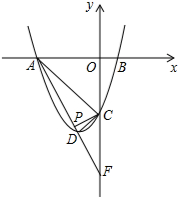
 如图,已知抛物线y=ax2+bx+c与x轴交于点A、B,与直线AC:y=-x-6交y轴于点C,点D是抛物线的顶点,且横坐标为-2.
如图,已知抛物线y=ax2+bx+c与x轴交于点A、B,与直线AC:y=-x-6交y轴于点C,点D是抛物线的顶点,且横坐标为-2.分析 (1)先由直线AC的解析式为y=-x-6,可得A(-6,0),C(0,-6),再根据抛物线的对称性求出B(2,0).然后把A、B、C三点坐标分别代入y=ax2+bx+c,利用待定系数法即可求解;
(2)先求出抛物线顶点D的坐标,再根据两点间的距离公式计算得出AC2=62+62=72,CD2=22+(-8+6)2=8,AD2=(-2+6)2+82=80,那么AC2+CD2=AD2,利用勾股定理的逆定理即可得到△ACD是直角三角形;
(3)先利用待定系数法求出直线AD的解析式为y=-2x-12,得到F(0,-12),设点P的坐标为(x,-2x-12).由∠ADC=∠DCF+∠DFC,∠PCF=∠DCF+∠PCD,∠ADC=∠PCF,可得∠DFC=∠PCD.根据两角对应相等的两三角形相似证明△CPD∽△FPC,那么$\frac{CP}{FP}$=$\frac{CD}{FC}$,依此列出比例式$\frac{{x}^{2}+(-2x-12+6)^{2}}{{x}^{2}+(2x)^{2}}$=$\frac{8}{{6}^{2}}$,解方程求出x的值,进而得到点P的坐标.
解答 解:(1)由直线AC:y=-x-6,可得A(-6,0),C(0,-6),
∵抛物线y=ax2+bx+c与x轴交于点A、B,抛物线的顶点D的横坐标为-2,
∴B(2,0).
把A、B、C三点坐标分别代入y=ax2+bx+c,得
$\left\{\begin{array}{l}{36a-6b+c=0}\\{4a+2b+c=0}\\{c=-6}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=2}\\{c=-6}\end{array}\right.$,
∴抛物线的解析式为y=$\frac{1}{2}$x2+2x-6;
(2)△ACD是直角三角形,理由如下:
∵y=$\frac{1}{2}$x2+2x-6=$\frac{1}{2}$(x+2)2-8,
∴顶点D的坐标是(-2,-8).
∵A(-6,0),C(0,-6),
∴AC2=62+62=72,CD2=22+(-8+6)2=8,AD2=(-2+6)2+82=80,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,∠ACD=90°; (3)假设在线段AD上存在一点P,使∠ADC=∠PCF.
(3)假设在线段AD上存在一点P,使∠ADC=∠PCF.
设直线AD的解析式为y=mx+n,
∵A(-6,0),D(-2,-8),
∴$\left\{\begin{array}{l}{-6m+n=0}\\{-2m+n=-8}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-2}\\{n=-12}\end{array}\right.$,
∴直线AD的解析式为y=-2x-12,
∴F点坐标为(0,-12),设点P的坐标为(x,-2x-12).
∵∠ADC=∠DCF+∠DFC,∠PCF=∠DCF+∠PCD,∠ADC=∠PCF,
∴∠DFC=∠PCD.
在△CPD与△FPC中,
$\left\{\begin{array}{l}{∠PCD=∠PFC}\\{∠CPD=∠FPC}\end{array}\right.$,
∴△CPD∽△FPC,
∴$\frac{CP}{FP}$=$\frac{CD}{FC}$,
∴$\frac{{x}^{2}+(-2x-12+6)^{2}}{{x}^{2}+(2x)^{2}}$=$\frac{8}{{6}^{2}}$,
整理得,35x2+216x+324=0,
解得x1=-$\frac{18}{7}$,x2=-$\frac{18}{5}$(舍去),
当x=-$\frac{18}{7}$时,-2x-12=-2×(-$\frac{18}{7}$)-12=-$\frac{48}{7}$,
故所求点P的坐标为(-$\frac{18}{7}$,-$\frac{48}{7}$).
点评 本题是二次函数的综合题型,其中涉及到利用待定系数法求二次函数、一次函数的解析式,二次函数的性质,勾股定理的逆定理,相似三角形的判定与性质等知识,综合性较强,难度适中.利用数形结合、方程思想是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
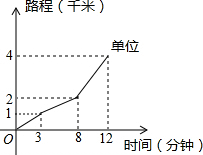 小张从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,则下列说法中正确的个数是( )
小张从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,则下列说法中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.25 | B. | 0.4 | C. | 0.45 | D. | 0.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
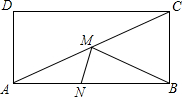 如图,在矩形ABCD中,AB=10,BC=5.若点M、N分别是线段AC,AB上的两个动点,则BM+MN的最小值为( )
如图,在矩形ABCD中,AB=10,BC=5.若点M、N分别是线段AC,AB上的两个动点,则BM+MN的最小值为( )| A. | 10 | B. | 8 | C. | 5$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
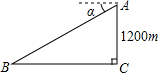 如图,某飞机在空中A处探测到它的正下方地平面上目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=30°,则飞机A与指挥台B的距离为( )
如图,某飞机在空中A处探测到它的正下方地平面上目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=30°,则飞机A与指挥台B的距离为( )| A. | 1200m | B. | 1200$\sqrt{2}$m | C. | 1200$\sqrt{3}$m | D. | 2400m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
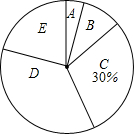 今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:| 分组 | 分数段(分) | 频数 |
| A | 36≤x<41 | 2 |
| B | 41≤x<46 | 5 |
| C | 46≤x<51 | 15 |
| D | 51≤x<56 | m |
| E | 56≤x<61 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com