
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 的一个交点是
的一个交点是![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
(2)设点![]() 是双曲线
是双曲线![]() 上一点,直线
上一点,直线![]() 与
与![]() 轴交于点
轴交于点![]() .若
.若![]() ,结合图象,直接写出点
,结合图象,直接写出点![]() 的坐标.
的坐标.
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(﹣ 2,﹣ 2),(![]() ,
, ![]() ),…,都是梦之点,显然梦之点有无数个.
),…,都是梦之点,显然梦之点有无数个.
(1)若点 P(2,b)是反比例函数![]() (n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(2)⊙ O 的半径是![]() ,
,

①求出⊙ O 上的所有梦之点的坐标;
②已知点 M(m,3),点 Q 是(1)中反比例函数![]() 图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,tan∠OAQ= 1.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,tan∠OAQ= 1.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想了解全校3000名同学对新闻、体育、音乐、娱乐、戏曲五类电视节目的喜爱情况,从中抽取了一部分同学进行了一次抽样调查,利用所得数据绘制成下面两幅不完整的统计图:
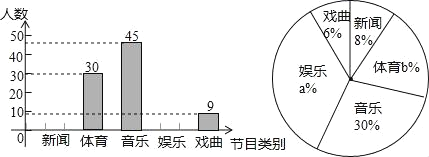
(1)在这次调查研究中,一共调查了 名学生,“体育”在扇形图中所占的圆心角是 度.
(2)求出右图中a、b的值,并补全条形图.
(3)若此次调查中喜欢体育节目的女同学有10人,请估算该校喜欢体育节目的女同学有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于点
相交于点![]() 和点
和点![]() 两点.
两点.
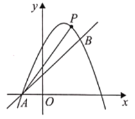
(1)求抛物线的函数表达式;
(2)若点![]() 是位于直线
是位于直线![]() 上方抛物线上的一动点,当
上方抛物线上的一动点,当![]() 的面积
的面积![]() 最大时,求此时
最大时,求此时![]() 的面积
的面积![]() 及点
及点![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是等腰三角形?若存在,直接写出
是等腰三角形?若存在,直接写出![]() 点的坐标(不用说理);若不存在,请说明理由.
点的坐标(不用说理);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的图形
中的图形![]() 和直线
和直线![]() ,给出如下定义:
,给出如下定义:![]() 为图形
为图形![]() 上任意一点,
上任意一点,![]() 为直线
为直线![]() 上任意一点,如果
上任意一点,如果![]() ,
,![]() 两点间的距离有最小值,那么称这个最小值为图形
两点间的距离有最小值,那么称这个最小值为图形![]() 和直线
和直线![]() 之间的“确定距离”,记作
之间的“确定距离”,记作![]() (
(![]() ,直线
,直线![]() ).
).
已知![]() ,
,![]() .
.
(1)求![]() (点
(点![]() ,直线
,直线![]() );
);
(2)![]() 的圆心为
的圆心为![]() ,半径为1,若
,半径为1,若![]() (
(![]() ,直线
,直线![]() )
)![]() ,直接写出
,直接写出![]() 的取值范围;
的取值范围;
(3)记函数![]() ,(
,(![]() ,
,![]() )的图象为图形
)的图象为图形![]() .若
.若![]() (
(![]() ,直线
,直线![]() )
)![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:将菱形的面积五等分.小红发现只要将菱形周长五等分,再将各分点与菱形的对角线交点连接即可解决问题.如图,点O是菱形ABCD的对角线交点,AB=5,下面是小红将菱形ABCD面积五等分的操作与证明思路,请补充完整.
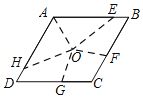
(1)在AB边上取点E,使AE=4,连接OA,OE;
(2)在BC边上取点F,使BF=______,连接OF;
(3)在CD边上取点G,使CG=______,连接OG;
(4)在DA边上取点H,使DH=______,连接OH.由于AE=______+______=______+______=______+______=______.可证S△AOE=S四边形EOFB=S四边形FOGC=S四边形GOHD=S△HOA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O在边AC上,⊙O与△ABC的边BC,AB分别相切于C,D两点,与边AC交于E点,弦CF与AB平行,与DO的延长线交于M点.
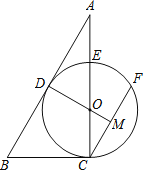
(1)求证:点M是CF的中点;
(2)若E是![]() 的中点,BC=a,写出求AE长的思路.
的中点,BC=a,写出求AE长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx﹣3(b是常数)经过点A(﹣1,0),(1)求抛物线的解析式_____.(2)P(m,t)为抛物线上的一个动点,P关于原点的对称点为P′,当点P′落在第二象限内,P′A2取得最小值时,求m的值_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com