
 阅读理解:
阅读理解:分析 (1)根据△ABP和△ABD的高相等,得到S△ABP=$\frac{1}{3}$S△ABD,根据△CDP和△CDA的高相等,得到S△CDP=$\frac{1}{3}$S△CDA,结合图形计算即可;
(2)仿照(1)的作法解答;
(3)根据AP=$\frac{1}{n}$AD,△ABP和△ABD的高相等,得到S△ABP=$\frac{1}{n}$S△ABD,PD=AD-AP=$\frac{n-1}{n}$AD,根据△CDP和△CDA的高相等,得到S△CDP=$\frac{n-1}{n}$S△CDA,整理即可;
(4)与(3)的解答方法类似,计算即可.
解答 解:(1)∵AP=$\frac{1}{3}$AD,△ABP和△ABD的高相等,
∴S△ABP=$\frac{1}{3}$S△ABD.
又∵PD=AD-AP=$\frac{1}{3}$AD,△CDP和△CDA的高相等,
∴S△CDP=$\frac{1}{3}$S△CDA.
∴S△PBC=S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD-$\frac{1}{3}$S△ABD-$\frac{1}{3}$S△CDA
=S四边形ABCD-$\frac{1}{3}$(S四边形ABCD-S△DBC)-$\frac{2}{3}$(S四边形ABCD-S△ABC)
=$\frac{1}{3}$S△DBC+$\frac{2}{3}$S△ABC.
∴S△PBC=$\frac{1}{3}$S△DBC+$\frac{2}{3}$S△ABC
(2)由(1)得,S△PBC=$\frac{1}{6}$S△DBC+$\frac{5}{6}$S△ABC;
(3)S△PBC=$\frac{1}{n}$S△DBC+$\frac{n-1}{n}$S△ABC;
∵AP=$\frac{1}{n}$AD,△ABP和△ABD的高相等,
∴S△ABP=$\frac{1}{n}$S△ABD.
又∵PD=AD-AP=$\frac{n-1}{n}$AD,△CDP和△CDA的高相等,
∴S△CDP=$\frac{n-1}{n}$S△CDA
∴S△PBC=S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD-$\frac{1}{n}$S△ABD-$\frac{n-1}{n}$S△CDA
=S四边形ABCD-$\frac{1}{n}$(S四边形ABCD-S△DBC)-$\frac{n-1}{n}$(S四边形ABCD-S△ABC)
=$\frac{1}{n}$S△DBC+$\frac{n-1}{n}$S△ABC.
∴S△PBC=$\frac{1}{n}$S△DBC+$\frac{n-1}{n}$S△ABC
(4)由(3)得,S△PBC=$\frac{b}{a}$S△DBC+$\frac{a-b}{a}$S△ABC.
点评 本题考查的是三角形的面积的计算,掌握高相等的两个三角形的面积比等于底的比是解题的关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:选择题
 周末,某小组12名同学都观看了电影《甲午风云》,其中8人买了甲票,4人买了乙票,总计用了200元.已知每张乙票比甲票售价多5元,求甲票、乙票的售价分别是多少元?设每张甲票的售价为x元,每张乙票的售价为y元.根据题意,可列方程组为( )
周末,某小组12名同学都观看了电影《甲午风云》,其中8人买了甲票,4人买了乙票,总计用了200元.已知每张乙票比甲票售价多5元,求甲票、乙票的售价分别是多少元?设每张甲票的售价为x元,每张乙票的售价为y元.根据题意,可列方程组为( )| A. | $\left\{\begin{array}{l}{x+5=y}\\{8x+4y=200}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-5=y}\\{8x+4y=200}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+5=y}\\{8x+4y=200}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-5=y}\\{4x+8y=200}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).
如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在⊙O的内接四边形ACDB中,AB为直径,AC:BC=1:2,点D为弧AB的中点,BE⊥CD垂足为E.
如图,在⊙O的内接四边形ACDB中,AB为直径,AC:BC=1:2,点D为弧AB的中点,BE⊥CD垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=10,BC=12,以AB为直径的⊙O交BC于点D.过点D的⊙O的切线垂直AC于点F,交AB的延长线于点E.
如图,在△ABC中,AB=10,BC=12,以AB为直径的⊙O交BC于点D.过点D的⊙O的切线垂直AC于点F,交AB的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
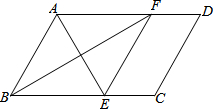 如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.
如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com