
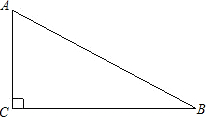
 (1)如图,要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮上画出一个半圆,使它的圆心O在线段AC上,且与AB、BC都相切.请你用直尺和圆规画出来(要求用尺规作图,保留作图痕迹,不要求写作法).
(1)如图,要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮上画出一个半圆,使它的圆心O在线段AC上,且与AB、BC都相切.请你用直尺和圆规画出来(要求用尺规作图,保留作图痕迹,不要求写作法). 解:(1)作出角平分线得(1分),作出半圆再得(1分),小结(1分),共(3分).
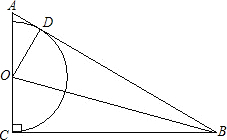
解:(1)作出角平分线得(1分),作出半圆再得(1分),小结(1分),共(3分).| 32+42 |
| 4 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| AD |
| AC |
| OD |
| BC |
| 1 |
| 3 |
| r |
| 4 |
| 4 |
| 3 |
| 8 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 8 |
| 3 |


科目:初中数学 来源: 题型:
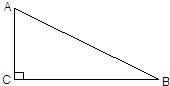 23、如图,要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮上画出一个半圆,使它的圆心在线段AC上,且与AB、BC都相切.请你用直尺和圆规画出来(要求用尺规作图,保留作图痕迹,不要求写作法).
23、如图,要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮上画出一个半圆,使它的圆心在线段AC上,且与AB、BC都相切.请你用直尺和圆规画出来(要求用尺规作图,保留作图痕迹,不要求写作法).查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,要在一块△ABC的纸片上截取正方形DEFG模型.其中,G、F在BC边上,D、E分别在AB、AC边上,AH⊥BC交DE于M,若BC=12cm,AH=8cm,则正方形DEFG的边长是( )
如图,要在一块△ABC的纸片上截取正方形DEFG模型.其中,G、F在BC边上,D、E分别在AB、AC边上,AH⊥BC交DE于M,若BC=12cm,AH=8cm,则正方形DEFG的边长是( )查看答案和解析>>
科目:初中数学 来源: 题型:
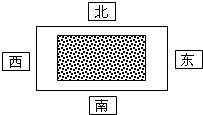 如图,要在一块长方形空地上设计一个花园,长方形空地长40米,宽30米,正中央的花园也是一个与整个场地长宽比例相同的长方形,花园四周是观光大道,如果要使四周观光大道的面积是花园面积的
如图,要在一块长方形空地上设计一个花园,长方形空地长40米,宽30米,正中央的花园也是一个与整个场地长宽比例相同的长方形,花园四周是观光大道,如果要使四周观光大道的面积是花园面积的| 9 | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com