
| A. | -1或4 | B. | -1 | C. | 1或4 | D. | 4 |
分析 分类讨论:当6为等腰三角形的底边,则方程有等根,所以△=(k+5)2-4(3k+6)=0,解得k1=k2=1,于是根据根与系数的关系得两腰的和=k+5=6,不满足三角形三边的关系,故舍去;当6为等腰三角形的腰,则x=6为方程的解,把x=6代入方程可计算出k的值.
解答 解:①当6为等腰三角形的底边,根据题意得△=(k+5)2-4(3k+6)=0,解得k1=k2=1,
此时,两腰的和=k+5=6,不满足三角形三边的关系,所以k1=k2=1舍去;
②当6为等腰三角形的腰,则x=6为方程的解,把x=6代入方程得36-6(k+5)+3k+6=0,解得k=4;
故选:D.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.也考查了等腰三角形的性质.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 杀伤半径 | 20≤x<40 | 40≤x<60 | 60≤x<80 | 80≤x<100 |
| 数量 | 8 | 12 | 25 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
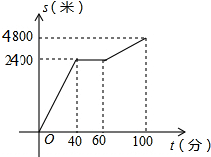 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走路程为s(米),s与t之间的函数关系如图所示,则下列说法中,错误的是( )
今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走路程为s(米),s与t之间的函数关系如图所示,则下列说法中,错误的是( )| A. | 小明中途休息用了20分钟 | |
| B. | 小明休息前爬山的速度为每分钟60米 | |
| C. | 小明在上述过程中所走路程为7200米 | |
| D. | 小明休息前后爬山的平均速度相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
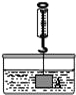 如图,在物理课上,小明用弹簧秤将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则如图能反映弹簧秤的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的大致图是( )
如图,在物理课上,小明用弹簧秤将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则如图能反映弹簧秤的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的大致图是( )| A. | 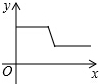 | B. | 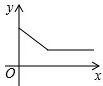 | C. | 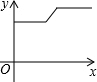 | D. | 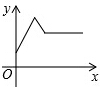 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 它的图象必经过点(-1,2) | B. | 它的图象经过第一、二、三象限 | ||
| C. | 当x>1时,y<0 | D. | y的值随x值的增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | 0 | 1 | 2 | 3 | … |
| y | … | -1 | 2 | 3 | 2 | … |
| A. | y1>y2 | B. | y1<y2 | ||
| C. | y1=y2 | D. | y1与y2大小无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
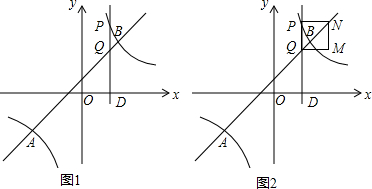
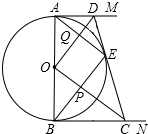 如图所示,AB是⊙O的直径,AM、BN是⊙O的两条切线,D、C分别在AM、BN上,DC切⊙O于点E,连接OD、OC、BE、AE,BE与OC相交于点P,AE与OD相交于点Q,已知AD=4,BC=9,以下结论:
如图所示,AB是⊙O的直径,AM、BN是⊙O的两条切线,D、C分别在AM、BN上,DC切⊙O于点E,连接OD、OC、BE、AE,BE与OC相交于点P,AE与OD相交于点Q,已知AD=4,BC=9,以下结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com