
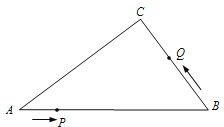
����Ŀ����ͼ����Rt��ABC�У���C��90��AB��10cm��AC��BC��4��3����P�ӵ�A������AB�������B�˶����ٶ�Ϊ1cm/s��ͬʱ��Q�ӵ�B������B��C��A�������A�˶����ٶ�Ϊ2cm/s����һ���˶��㵽���յ�ʱ����һ���˶���Ҳ��ֹ֮ͣ�˶���
��1�����P���˶�ʱ��Ϊx���룩����PBQ�����Ϊy��cm2��������PBQ����ʱ����y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2����x��5��ʱ����ֱ��PQ���Ƿ����һ��M��ʹ��BCM���ܳ���С�������ڣ������С�ܳ����������ڣ���˵�����ɣ�
��3������Q��BC�����˶�ʱ���Ƿ����x��ʹ������PBQ��һ������ΪԲ����Բʱ��������������������Բ�ϣ������ڣ���� x��ֵ�������ڣ�˵������.
���𰸡�(1)��y=��![]() ��8x��0��x��3����y=
��8x��0��x��3����y=![]() ��(2)��16��(3)��x=
��(2)��16��(3)��x=![]() .
.
��������
���������(1)���ֵ�Q�ڱ�BC�Ϻ͵�Q�ڱ�CA���˶���(2)������AQ=14��2x=14��10=4��AP=x=5�Լ�AC=8��AB=10���Ӷ��ó�PQ��AC�Ĵ�ֱƽ���ߣ���PC=AP=5��������M��P�غ�ʱ����BCM���ܳ���С��(3)��������Ҫ����������ó���.
���������(1)��������Q�ڱ�BC���˶�ʱ��y=��![]() ��8x��0��x��3����
��8x��0��x��3����
������Q�ڱ�CA���˶�ʱ��y=![]() =
=![]() ��3��x��7����
��3��x��7����

(2)�����ڣ� ���ɣ���AQ=14��2x=14��10=4��AP=x=5�� ��AC=8��AB=10��
��PQ����ABC����λ�ߣ� ��PQ��AB����PQ��AC�� ��PQ��AC�Ĵ�ֱƽ���ߣ�
��PC=AP=5�� ������M��P�غ�ʱ����BCM���ܳ���С��
���BCM���ܳ�Ϊ�� MB��BC��MC��PB��BC��PC=5��6��5=16�� ���BCM���ܳ���СֵΪ16��
(3)�����������PBQ����������
��PQ=PB,x=![]() ��3(��) ��BQ=BP��x=
��3(��) ��BQ=BP��x=![]() ��3���ᣩ ��QP=QB,x=
��3���ᣩ ��QP=QB,x=![]() ��
��
�����������������������x��x=![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ӹ�һ�����������20������ÿ��ӹ�����������ʾ��
ÿ��ӹ������ | 4 | 5 | 6 | 7 | 8 |
���� | 3 | 6 | 5 | 4 | 2 |
ÿ��ӹ����������λ��������Ϊ��������
A.6��5B.6��6C.5��5D.5��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
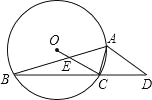
����Ŀ����ͼ��ʾ����O���ڽ���ABC�У���BAC=45������ABC=15����AD��OC����BC���ӳ�����D�㣬OC��AB��E�㣮
��1������D�Ķ�����
��2����֤��AC2=ADCE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����(1)��3.56 ���Ǹ�����������Ҳ����������(2)������������ͳ��Ϊ������(3)0 �Ƿ�������(4)��2018 ���Ǹ�����Ҳ����������������������5����Ȼ����������������ȷ�ĸ����ǣ� ��
A. 4 B. 3 C. 2 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
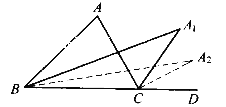
����Ŀ����ͼ����![]() ABC�У�
ABC�У� ![]() A=80
A=80![]() ��
�� ![]() ABC��
ABC��![]() ACD��ƽ���߽��ڵ�A1����
ACD��ƽ���߽��ڵ�A1����![]() A1��
A1�� ![]() A1BC��
A1BC��![]() A1CD��ƽ�����ཻ�ڵ�A2����
A1CD��ƽ�����ཻ�ڵ�A2����![]() A2��������
A2�������� ![]() A7BC��
A7BC��![]() A7CD��ƽ�����ཻ�ڵ�A8����
A7CD��ƽ�����ཻ�ڵ�A8����![]() A8����
A8����![]() A8�Ķ���Ϊ����
A8�Ķ���Ϊ����
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��a+b=4��ab=1��
��1����a��b��2��ֵ�� ��2��a5b��2a4b4+ab5��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ģ�ʮ�������ҺӴ�Ϲ�ϲ����գ���ũ�������ջ�����20�֣����12�֣��ּƻ����üס������ֻ�����8���������Ϲ�ȫ������������ۣ���֪һ�����ֻ�����װ����4�ֺ����1�֣�һ�����ֻ�����װ���Ϻ���ϸ�2�֣�
��1����ũ��������ΰ��żס������ֻ�����һ���Ե��˵����۵أ��м��ַ�����
��2�������ֻ���ÿ��Ҫ�������300Ԫ�����ֻ���ÿ��Ҫ�������240Ԫ�����ũ������Ӧѡ�����ַ�����ʹ��������٣������˷��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ��Բ�Ľ�Ϊ108�����뾶Ϊ4cm������ֽƬ��С���ȥԲ�Ľ�Ϊ���IJ�������ֽƬ��ʣ�µ�ֽƬ������һ������뾶Ϊ1cm��Բ��ֽñ���ӷ촦���ص��������ȥ������ֽƬ�����Ϊ�� ��.
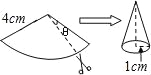
A��0.8��cm2 B��3.2��cm2 C��4��cm2 D��4.8��cm2
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com