
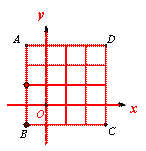
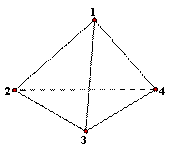
����ƽ��ֱ������ϵ�е�������ABCD�ı߳�Ϊ4����������ʵ�飺����һö���ȵ������������ӣ���ͼ�������ĸ����㣬���������ֱ���1��2��3��4���� ÿ�����㳯�ϵĻ�������ͬ�ģ������������Σ������ӳ��ϵĵ�����Ϊֱ������ϵ�е�P�����꣨��һ�εĵ���Ϊ�����꣬�ڶ��εĵ���Ϊ�����꣩��
��1�����P�������������ϣ����߽磬��ͬ���ĸ��ʡ�
 ��2����������ABCDƽ��������λ���Ƿ����һ��ƽ�ƣ�ʹ��P�������������ϵĸ���Ϊ
��2����������ABCDƽ��������λ���Ƿ����һ��ƽ�ƣ�ʹ��P�������������ϵĸ���Ϊ![]() �������ڣ�ָ�����е�һ��ƽ�Ʒ�ʽ���������ڣ�˵�����ɣ�
�������ڣ�ָ�����е�һ��ƽ�Ʒ�ʽ���������ڣ�˵�����ɣ�

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ʹ��B���ڱ�OA�ĵ�D������֪�ۺ�CE=5
��ʹ��B���ڱ�OA�ĵ�D������֪�ۺ�CE=5| 5 |
| 3 |
| 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
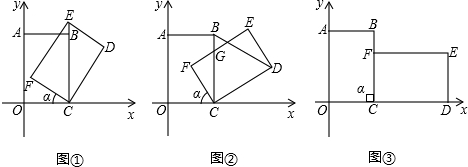
 OABC��һ�ŷ���ƽ��ֱ������ϵ�еľ���ֽƬ��OΪԭ�㣬��A��x���ϣ���C��y���ϣ�OA=10��OC=6��
OABC��һ�ŷ���ƽ��ֱ������ϵ�еľ���ֽƬ��OΪԭ�㣬��A��x���ϣ���C��y���ϣ�OA=10��OC=6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
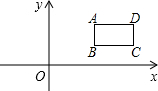 ��ͼ������Ϊ3cm�ľ���ABCD����ƽ��ֱ������ϵ�У�����D��6��3������A�������Ϊ��������
��ͼ������Ϊ3cm�ľ���ABCD����ƽ��ֱ������ϵ�У�����D��6��3������A�������Ϊ��������| A����5��3�� | B����4��3�� | C����4��2�� | D����3��3�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com