
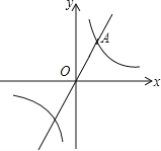
【题目】 如图,已知正比例函数y=kx与反比例函数y=![]() 的图象在第一象限交于点A(2,4).
的图象在第一象限交于点A(2,4).
(1)求正比例函数与反比例函数的解析式.
(2)平移直线OA,平移后的直线与x轴交于点B,与反比例函数的图象交于第一象限的点C(4,n).
①求直线BC的解析式;
②线段BC的长是______.
【答案】(1)正比例函数的解析式为y=2x,反比例函数的解析式为y=![]() ;(2)①y=2x-6;②
;(2)①y=2x-6;②![]() .
.
【解析】
(1)将点A的坐标分别代入y=kx与y=![]() ,即可得出正比例函数与反比例函数的解析式;
,即可得出正比例函数与反比例函数的解析式;
(2)①利用已知的反比例函数的解析式,可得出n的值;设平移后的一次函数解析式,代入点C的坐标,即可得出直线BC的解析式;
②先求出点B的坐标,再利用两点间的距离公式,即可得出线段BC的长.
解:(1)∵正比例函数y=kx与反比例函数y=![]() 的图象在第一象限交于点A(2,4),
的图象在第一象限交于点A(2,4),
∴4=2k,4=![]() ,
,
解得:k=2,m=8,
∴正比例函数的解析式为y=2x,反比例函数的解析式为y=![]() ;
;
(2)①∵点C(4,n)在反比例函数y=![]() 的图象上,
的图象上,
∴n=![]() =2,
=2,
即点C的坐标为(4,2).
∵AO∥BC,
∴可设直线BC的解析式为y=2x+b,
又点C(4,2)在直线BC上,
∴2=2×4+b,
解得b=-6,
即直线BC的解析式为y=2x-6;
②∵直线BC与x轴交于点B,
∴当y=0时,0=2x-6,
解得x=3,
∴点B的坐标为(3,0),
∵C(4,2),
∴BC=![]() =
=![]() .
.
故答案为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
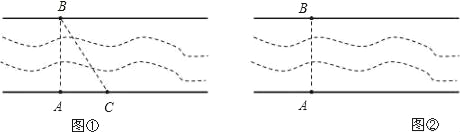
【题目】经过江汉平原的沪蓉(上海﹣成都)高速铁路即将动工.工程需要测量汉江某一段的宽度.如图①,一测量员在江岸边的A处测得对岸岸边的一根标杆B在它的正北方向,测量员从A点开始沿岸边向正东方向前进100米到达点C处,测得∠ACB=68°.
(1)求所测之处江的宽度(sin68°≈0.93,cos68°≈0.37,tan68°≈2.48.);
(2)除(1)的测量方案外,请你再设计一种测量江宽的方案,并在图②中画出图形.(不用考虑计算问题,叙述清楚即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+4x+c的图象与x轴交于A、B两点,与y轴交于点C,其中A(﹣1,0),C(0,5)
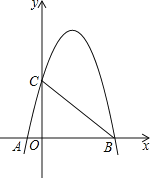
(1)求二次函数的解析式,并求出当x=1时的函数值.
(2)连接BC,AC,得到△ABC,现将抛物线图象只向下平移m个单位,使得顶点落在△ABC内部(不包括边界),请写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是![]() 的中点,连接AE交BC于点F,∠ACB=2∠EAB.
的中点,连接AE交BC于点F,∠ACB=2∠EAB.

(1)求证:AC是⊙O的切线;
(2)若cosC=![]() ,AC=6,求BF的长.
,AC=6,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=70°,以B为圆心,任意长为半径画弧交AB,BC于点E,F,再分别以点E,F为圆心、以大于![]() EF长为半径画弧,两弧交于点P,作射线BP交AC于点D,则∠BDC为( )度.
EF长为半径画弧,两弧交于点P,作射线BP交AC于点D,则∠BDC为( )度.

A. 65 B. 75 C. 80 D. 85
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A.概率是1%的事件在一次试验中一定不会发生
B.要了解某公司生产的100万只灯泡的使用寿命,可以采用全面调查的方式
C.甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62,则乙的成绩更稳定
D.随意翻到一本书的某页,页码是奇数是随机事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题:
观察下列方程:①![]() ;②
;②![]() ;③
;③![]() ;…;
;…;
(1)按此规律写出关于x的第4个方程为 ,第n个方程为 ;
(2)直接写出第n个方程的解,并检验此解是否正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
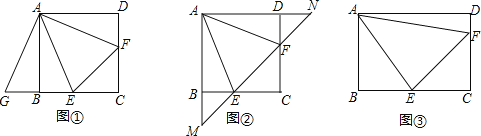
【题目】正方形![]() 中,点
中,点![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() .
.
(1)将![]() 绕着点
绕着点![]() 顺时针旋转90°,得到
顺时针旋转90°,得到![]() (如图①),求证:
(如图①),求证:![]() ;
;
(2)若直线![]() 与
与![]() ,
,![]() 的延长线分别交于点
的延长线分别交于点![]() (如图②),求证:
(如图②),求证:![]() ;
;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系 .(不要求书写证明过程)
之间的数量关系 .(不要求书写证明过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com