练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在Rt△ACB中，∠C=90°，AC=BC，一直角三角板的直角顶角O在AB边的中点上，这块三角板绕O点旋转，两条直角边始终与AC、BC边分别相交于E、F，连接EF，则在运动过程中，△OEF与△ABC的关系是（　　）

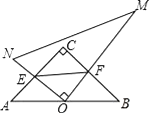
    A. 一定相似 B. 当E是AC中点时相似

    C. 不一定相似 D. 无法判断

    【答案】A

    【解析】试题解析：连结OC，

    ∵∠C=90°，AC=BC，

    ∴∠B=45°，

    ∵点O为AB的中点，

    ∴OC=OB，∠ACO=∠BCO=45°，

    ∵∠EOC+∠COF=∠COF+∠BOF=90°，

    ∴∠EOC=∠BOF，

    在△COE和△BOF中，

    ∴△COE≌△BOF（ASA），

    ∴OE=OF，

    ∴△OEF是等腰直角三角形，

    ∴∠OEF=∠OFE=∠A=∠B=45°，

    ∴△OEF∽△△CAB．

    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图(1)，AB∥CD，猜想∠BPD与∠B.∠D的关系，说明理由．(提示：三角形的内角和等于180°)

    ①填空或填写理由

    解：猜想∠BPD+∠B+∠D=360°

    理由：过点P作EF∥AB，

    ∴∠B+∠BPE=180°______

    ∵AB∥CD，EF∥AB，

    ∴______∥_____，(如果两条直线都和第三条直线平行，那么这两条直线也互相平行)

    ∴∠EPD+______=180°

    ∴∠B+∠BPE+∠EPD+∠D=360°

    ∴∠B+∠BPD+∠D=360°

    ②依照上面的解题方法，观察图(2)，已知AB∥CD，猜想图中的∠BPD与∠B.∠D的关系，并说明理由．

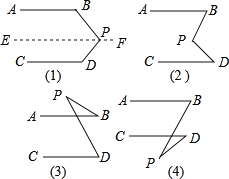
    ③观察图(3)和(4)，已知AB∥CD，直接写出图中的∠BPD与∠B.∠D的关系，不说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

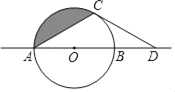
    【题目】如图，⊙O半径为1，AB是⊙O的直径，C是⊙O上一点，连接AC，⊙O外的一点D 在直线AB上．

    （1）若AC=，OB=BD．

    ①求证：CD是⊙O的切线．

    ②阴影部分的面积是　 　．（结果保留π）

    （2）当点C在⊙O上运动时，若CD是⊙O的切线，探究∠CDO与∠OAC的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场在黄金周促销期间规定：商场内所有商品按标价的打折出售；同时，当顾客在该商场消费打折后的金额满一定数额，还可按如下方案抵扣相应金额：

    说明：表示在范围中，可以取到a，不能取到b．

    根据上述促销方法，顾客在该商场购物可以获得双重优惠：打折优惠与抵扣优惠．

    例如：购买标价为900元的商品，则打折后消费金额为450元，获得的抵扣金额为30元，总优惠额为：元，实际付款420元．

    购买商品得到的优惠率，

    请问：

    购买一件标价为500元的商品，顾客的实际付款是多少元？

    购买一件商品，实际付款375元，那么它的标价为多少元？

    请直接写出，当顾客购买标价为______元的商品，可以得到最高优惠率为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

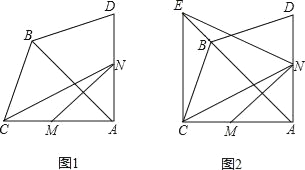
    【题目】如图1，在△ABC中，AB=AC=4，∠ABC=67.5°，△ABD和△ABC关于AB所在的直线对称，点M为边AC上的一个动点（重合），点M关于AB所在直线的对称点为N，△CMN的面积为S．

    （1）求∠CAD的度数；

    （2）设CM=x，求S与x的函数表达式，并求x为何值时S的值最大？

    （3）S的值最大时，过点C作EC⊥AC交AB的延长线于点E，连接EN（如图2），P为线段EN上一点，Q为平面内一点，当以M，N，P，Q为顶点的四边形是菱形时，请直接写出所有满足条件NP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料:

    根据绝对值的定义，|x| 表示数轴上表示数x的点与原点的距离，那么，如果数轴上两点P、Q表示的数为x1，x2时，点P与点Q之间的距离为PQ=|x1-x2|.

    根据上述材料，解决下列问题:

    如图，在数轴上，点A、B表示的数分别是-4, 8(A、B两点的距离用AB表示)，点M、N是数轴上两个动点，分别表示数m、n.

    (1)AB=_____个单位长度；若点M在A、B之间，则|m+4|+|m-8|=______；

    (2)若|m+4|+|m-8|=20，求m的值；

    (3)若点M、点N既满足|m+4|+n=6，也满足|n-8|+m=28，则m= ____ ；n=______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

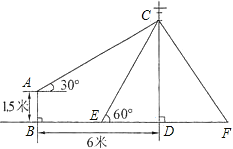
    【题目】如图，在电线杆上的C处引拉线CE、CF固定电线杆，拉线CE和地面成60°角，在离电线杆6米的B处安置测角仪，在A处测得电线杆上C处的仰角为30°，已知测角仪高AB为1.5米，求拉线CE的长（结果保留根号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

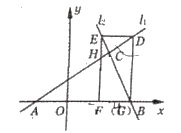
    【题目】如图，已知直线：与直线：相交于点，直线、分别交轴于、两点，矩形的顶点、分别在、上，顶点、都在轴上，且点与点重合，那么 __________________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在四边形ABCD中如图，∠A＝∠B＝90°，将△AED、△DCF分别沿着DE、DF翻折，点A、C都分别与EF上的点G重合．

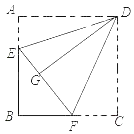
    （1）求证：四边形ABCD是正方形；（2）若AB＝6，点F是BC的中点，求AE的长．

    查看答案和解析>>

    同步练习册答案