Question

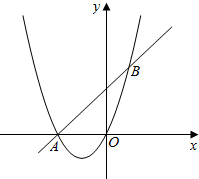
9．二次函数y₁═ax²+2x过点A（-2，0）、与点O和点B，过点A，B作一次函数y₂=kx+b，若点B的横坐标为1．
（1）求出二次函数与一次函数的解析式；
（2）直接写出y₂＞y₁时，x的取值范围；
（3）在抛物线上，是否存在一点P，使△PAB的面积等于△ABO的面积？若存在求出P点坐标，若不存在，说明理由．

Answer 1

分析 （1）如图1，利用待定系数法求二次函数与一次函数的解析式；
（2）如图1，根据图象直接写出y₂＞y₁时，-2＜x＜1；
（3）如图2，观察△PAB和△ABO，有一公共边AB，由平行线的距离相等，和同底边等高的两三角形面积相等作AB的两条平行线，这两条平行线与抛物线的交点就是点P，这样的P点有三个符合题意．

解答 解：（1）如图1，把A（-2，0）代入y₁═ax²+2x中得：4a+2×（-2）=0，
a=1，
∴二次函数的解析式y₁═x²+2x，
当x=1时，y₁=1+2=3，
∴B（1，3），
把A（-2，0）、B（1，3）代入y₂=kx+b中得：$\left\{\begin{array}{l}{-2k+b=0}\\{k+b=3}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$，
∴一次函数的解析式：y₂=x+2，
则二次函数解析式为：y₁═x²+2x，一次函数的解析式为y₂=x+2；
（2）如图1，由图象得：当-2＜x＜1时，y₂＞y₁；
（3）如图2，存在，
过O作OP₁∥AB，交抛物线于P₁，
则OP₁的解析式为：y=x，
∴$\left\{\begin{array}{l}{y=x}\\{y={x}^{2}+2x}\end{array}\right.$，
x²+2x=x，
x（x+1）=0，
x₁=0（舍），x₂=-1，
当x₂=-1时，y=-1，
∴P₁（-1，-1），
当x=0时，y=2，
∴C（0，2），
∴在y轴取一点D（0，4），过D作DP₂∥AB，交抛物线于P₂、P₃，
则DP₂的解析式为：y=x+4，
∴$\left\{\begin{array}{l}{y=x+4}\\{y={x}^{2}+2x}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{{x}_{1}=\frac{-1+\sqrt{17}}{2}}\\{{y}_{1}=\frac{7+\sqrt{17}}{2}}\end{array}\right.$   $\left\{\begin{array}{l}{{x}_{2}=\frac{-1-\sqrt{17}}{2}}\\{{y}_{2}=\frac{7-\sqrt{17}}{2}}\end{array}\right.$，
∴P₂（$\frac{-1-\sqrt{17}}{2}$，$\frac{7-\sqrt{17}}{2}$），P₃（$\frac{-1+\sqrt{17}}{2}$，$\frac{7+\sqrt{17}}{2}$），
综上所述，当P₁（-1，-1）或P₂（$\frac{-1-\sqrt{17}}{2}$，$\frac{7-\sqrt{17}}{2}$）或P₃（$\frac{-1+\sqrt{17}}{2}$，$\frac{7+\sqrt{17}}{2}$）时，△PAB的面积等于△ABO的面积．

点评 本题是二次函数的综合题，考查了利用待定系数法求二次函数与一次函数的解析式；是常考题型，同时采用数形结合的方式解决问题，如第二问直接由图象得出x的取值范围；对于第（3）问的面积问题，要看清是哪两个三角形，有时会给出△AOB和△AOP的面积相等，这样要简单一些，本题是△PAB的面积等于△ABO的面积，由平行线保证等高来解决问题，同时运用了两直线平行，则一次项系数相等这一结论．