
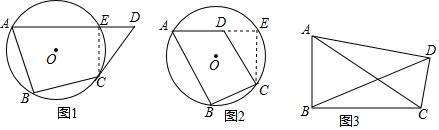
分析 (1)材料中划线部分结论的依据圆的内接四边形对角互补,
(2)证明过程中分点D在圆外或圆内两种情形讨论,主要体现了分类讨论的数学思想.
(3)利用“对角互补的四边形的四个顶点能作一个圆”这个结论,结合直径的性质以及等腰三角形的性质,即可解决问题.
解答 解:(1)材料中划线部分结论的依据圆的内接四边形对角互补,
故答案为材料中划线部分结论的依据
(2)证明过程中主要体现了分类讨论的数学思想,分点D在圆外或圆内两种情形讨论.
故答案为D;
(3)解:∵∠ABC+∠ADC=180°,
∴过四边形ABCD的四个顶点能作一个圆(如图所示),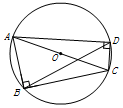
∴∠CBD=∠CAD=16°,
∴∠ABD=74°,
又∵AD=BD,
∴∠BAD=∠ABD=74°,
∴∠ADB=32°.
点评 本题考查圆综合题、推导了对角互补的四边形的四个顶点能作一个圆,解题的关键是利用结论解决问题,属于中考创新题目.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
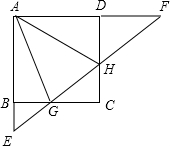 如图,正方形ABCD的边长为4,点G、H分别是BC、CD边上的点,直线GH与AB、AD的延长线相交于点E、F,连接AG、AH.
如图,正方形ABCD的边长为4,点G、H分别是BC、CD边上的点,直线GH与AB、AD的延长线相交于点E、F,连接AG、AH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com