
【题目】在平面直角坐标系中,O为原点,点A(﹣2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α.

(1)如图①,当α=90°时,求AE′,BF′的长;
(2)如图②,当α=135°时,求证AE′=BF′,且AE′⊥BF′;
(3)若直线AE′与直线BF′相交于点P,求点P的纵坐标的最大值(直接写出结果即可).
【答案】(1)AE′=![]() ,BF′=
,BF′=![]() ;(2)答案见解析;(3)
;(2)答案见解析;(3)![]() .
.
【解析】试题分析:(1)利用勾股定理即可求出![]() 的长.
的长.
(2)运用全等三角形的判定与性质、三角形的外角性质就可解决问题.
(3)首先找到使点P的纵坐标最大时点P的位置(点P与点D′重合时),然后运用勾股定理及30°角所对的直角边等于斜边的一半等知识即可求出点P的纵坐标的最大值.
试题解析:(Ⅰ)当![]() 时,点E′与点F重合,如图①,
时,点E′与点F重合,如图①,
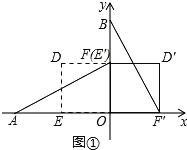
∵点A(2,0)点B(0,2),
∴OA=OB=2.
∵点E,点F分别为OA,OB的中点,
∴OE=OF=1,
∵正方形OE′D′F′是正方形OEDF绕点O顺时针旋转![]() 得到的,
得到的,
∴OE′=OE=1,OF′=OF=1.
在Rt△AE′O中,
![]()
在Rt△BOF′中,
![]()
∴AE′,BF′的长都等于![]()
(Ⅱ)当![]() 时,如图②,
时,如图②,
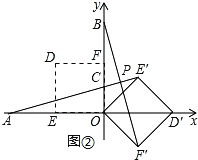
∵正方形OE′D′F′是由正方形OEDF绕点O顺时针旋转![]() 所得,
所得,
![]()
在△AOE′和△BOF′中,
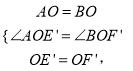
∴△AOE′≌△BOF′(SAS).
∴AE′=BF′,且∠OAE′=∠OBF′.
∵∠ACB=∠CAO+∠AOC=∠CBP+∠CPB,∠CAO=∠CBP,
![]()
∴AE′⊥BF′.
(Ⅲ) ![]() ,∴点P、B. A.O四点共圆,
,∴点P、B. A.O四点共圆,

∴当点P在劣弧OB上运动时,点P的纵坐标随着∠PAO的增大而增大,
∵OE′=1,∴点E′在以点O为圆心,1为半径的![]() 上运动,
上运动,
∴当AP与![]() 相切时,∠E′AO(即∠PAO)最大,
相切时,∠E′AO(即∠PAO)最大,
此时![]() 点D′与点P重合,点P的纵坐标达到最大,
点D′与点P重合,点P的纵坐标达到最大,
过点P作PH⊥x轴,垂足为H,如图③所示,
![]()
![]()
![]()
![]()
![]()
∴点P的纵坐标的最大值为![]()


科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中A(a,0),B(0,b),且a,b满足![]() .
.


(1) (2)
(1)A、B坐标分别为A( ) 、B( ).
(2)P为x轴上一点,C为AB中点,∠APC=∠PBO,求AP的长.
(3)如图2,点E为第一象限一点,AE=AB,以AE为斜边构造等腰直角△AFE,连BE,连接OF并延长交BE于点G,求证:BG=EG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3![]() 、7
、7![]() 、9
、9![]() ;乙盒子中装有4张卡片,卡片上分别写着2
;乙盒子中装有4张卡片,卡片上分别写着2![]() 、4
、4![]() 、6
、6![]() 、8
、8![]() ;盒子外有一张写着5
;盒子外有一张写着5![]() 的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果生产基地,某天安排30名工人采摘枇杷或草莓(每名工人只能做其中一项工作),并且每人每天摘0.4吨枇杷或0.3吨草莓,当天的枇杷售价每吨2000元,草莓售价每吨3000元,设安排其中x名工人采摘枇杷,两种水果当天全部售出,销售总额达y元.
(1)求y与x之间的函数关系式;
(2)若要求当天采摘枇杷的数量不少于草莓的数量,求销售总额的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校提倡练字,小冬和小红一起去文具店买钢笔和字帖,小冬在文具店买1支钢笔和3本字帖共花了38元,小红买了2支钢笔和4本字帖共花了64元.
(1)每支钢笔与每本字帖分别多少元?
(2)帅帅在六一节当天去买,正巧碰到文具店搞促销,促销方案有两种形式:
①所购商品均打九折
②买一支钢笔赠送一本字帖
帅帅要买5支钢笔和15本字帖,他有三种选择方案:
(Ⅰ)一次买5支钢笔和15本字帖,然后按九折付费;
(Ⅱ)一次买5支钢笔和10本字帖,文具店再赠送5本字帖;
(Ⅲ)分两次购买,第一次买5支钢笔,文具店会赠送5本字帖,第二次再去买10本字帖,可以按九折付费;问帅帅最少要付多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
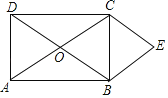
【题目】平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.
(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;
(2)当四边形ABCD是 形时,四边形OBEC是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校教职工为庆祝“建国![]() 周年”开展学习强国知识竞赛,本次知识竞赛分为甲、乙、丙三组进行.下面两幅统计图反映了教师参加学习强国知识竞赛的报名情况,请你根据图中的信息回答下列问题:
周年”开展学习强国知识竞赛,本次知识竞赛分为甲、乙、丙三组进行.下面两幅统计图反映了教师参加学习强国知识竞赛的报名情况,请你根据图中的信息回答下列问题:
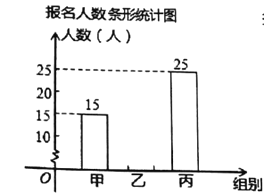
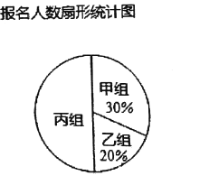
(1)该校教师报名参加本次学习强国知识竞赛的总人数为___________人,并补全条形统计图;
(2)该校教师报名参加丙组的人数所占圆心角度数是__________;
(3)根据实际情况,需从甲组抽调部分教师到丙组,使丙组人数是甲组人数的![]() 倍,应从甲组抽调多少名教师到丙组?
倍,应从甲组抽调多少名教师到丙组?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com