
【题目】如图,抛物线y= ![]() x(x﹣k)经过原点O,交x轴正半轴于A,过A的直线交抛物线于另一点B,AB交y轴正半轴于C,且OC=OA,B点的纵坐标为9
x(x﹣k)经过原点O,交x轴正半轴于A,过A的直线交抛物线于另一点B,AB交y轴正半轴于C,且OC=OA,B点的纵坐标为9
(1)求抛物线的解析式;
(2)点P为第一象限的抛物线上一点,连接PB、PC,设P点的横坐标为m,△PBC的面积为S,求S与m的函数关系式;
(3)在(2)的条件下,连接OP、AP,若∠APO=45°,求点P的坐标.
【答案】
(1)
解:如图1中,作BH⊥x轴于H.
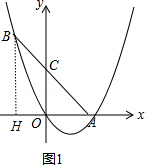
由题意OC=OA=K,∠AOC=90°,
∴∠OAC=∠OCA=45°,
∵∠BHA=90°,
∴∠HBA=∠HAB=45°,
∴BH=AH=9,
∴OH=9﹣k,
∴B(k﹣9,9),
把B(k﹣9,9)代入y= ![]() x(x﹣k),
x(x﹣k),
得到9= ![]() (k﹣9)×(﹣9),
(k﹣9)×(﹣9),
∴k=5,
∴抛物线的解析式为y= ![]() x(x﹣5).
x(x﹣5).
(2)
解:如图2中,作BH⊥x轴于H,连接OP、PH、PA.设P[m, ![]() m(m﹣5)].
m(m﹣5)].
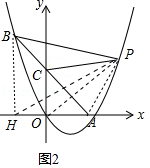
∵P(﹣4,9),A(5,0),C(0,5),
∴S△PBC=S△PAB﹣S△PCA=(S△PBH+S△PHA﹣S△ABH)﹣(S△PCO+S△POA﹣S△AOC)
= ![]() ×9×(m+4)+
×9×(m+4)+ ![]() ×9×
×9× ![]() m(m﹣5)﹣
m(m﹣5)﹣ ![]() ×9×9﹣[
×9×9﹣[ ![]() ×5×m+
×5×m+ ![]() ×5×
×5× ![]() m(m﹣5)﹣
m(m﹣5)﹣ ![]() ×5×5]
×5×5]
= ![]() m2﹣m﹣10(m>5).
m2﹣m﹣10(m>5).
(3)
解:如图3中设AC交OP于D,AC的中点为K,连接PK.
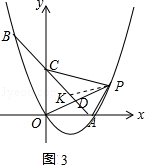
∵∠DPA=∠DCO=45°,∠PDA=CDO,
∴△PDA∽△CDO,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,∵∠CDP=∠ODP,
,∵∠CDP=∠ODP,
∴△CDP∽△ODA,
∴∠CPD=∠OAD=45°,
∴∠CPA=90°,
∵CK=KA,
∴PK= ![]() AC=
AC= ![]() ,
,
设P[m, ![]() m(m﹣5)],
m(m﹣5)],
∵K( ![]() ,
, ![]() ),
),
∴(m﹣ ![]() )2+[
)2+[ ![]() m(m﹣5)﹣
m(m﹣5)﹣ ![]() ]2=(
]2=( ![]() )2,
)2,
整理得m(m﹣5)(m2﹣5m﹣4)=0,
∴m=0或5或 ![]() 或
或 ![]() ,
,
∵m>5,
∴m= ![]() ,
,
∴P( ![]() ,1).
,1).
【解析】(1)如图1中,作BH⊥x轴于H.由题意OC=OA=K,∠AOC=90°,推出∠OAC=∠OCA=45°,由∠BHA=90°,推出∠HBA=∠HAB=45°,推出BH=AH=9,推出OH=9﹣k,推出B(k﹣9,9),把B(k﹣9,9)代入y= ![]() x(x﹣k),解方程即可.(2)如图2中,作BH⊥x轴于H,连接OP、PH、PA.设P[m,
x(x﹣k),解方程即可.(2)如图2中,作BH⊥x轴于H,连接OP、PH、PA.设P[m, ![]() m(m﹣5)].根据S△PBC=S△PAB﹣S△PCA=(S△PBH+S△PHA﹣S△ABH)﹣(S△PCO+S△POA﹣S△AOC)计算即可.(3)如图3中设AC交OP于D,AC的中点为K,连接PK.只要证明∠CPA=90°,根据PK=
m(m﹣5)].根据S△PBC=S△PAB﹣S△PCA=(S△PBH+S△PHA﹣S△ABH)﹣(S△PCO+S△POA﹣S△AOC)计算即可.(3)如图3中设AC交OP于D,AC的中点为K,连接PK.只要证明∠CPA=90°,根据PK= ![]() ,利用两点间距离公式,列出方程,解方程即可解决问题.
,利用两点间距离公式,列出方程,解方程即可解决问题.
【考点精析】本题主要考查了等腰直角三角形和函数关系式的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;用来表示函数关系的数学式子叫做函数解析式或函数关系式才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG. 
(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG; 
(2)如图3,如果α=45°,AB=2,AE=4 ![]() ,求点G到BE的距离.
,求点G到BE的距离. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威丽商场销售A,B两种商品,售出1件A种商品和4件B种商品所得利润为600元,售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元;
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件.如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航行,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由.(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2是两张形状大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,线段AB、EF的端点均在小正方形的顶点上.
(1)如图1,作出以AB为对角线的正方形并直接写出正方形的周长; 
(2)如图2,以线段EF为一边作出等腰△EFG(点G在小正方形顶点处)且顶角为钝角,并使其面积等于4. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)过A(4,4),B(2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是( )
A.m≤2或m≥3
B.m≤3或m≥4
C.2<m<3
D.3<m<4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=2+ ![]() .
.
(1)写出自变量x的取值范围:;
(2)请通过列表,描点,连线画出这个函数的图象: ①列表:
x | … | ﹣8 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | ﹣ | | 1 | 2 | 3 | 4 | 8 | … |
y | … | | 1 | | 0 | ﹣2 | ﹣6 | 10 | 6 | 4 | | 3 | | … |
②描点(在下面给出的直角坐标系中补全表中对应的各点);
③连线(将图中描出的各点用平滑的曲线连接起来,得到函数的图象).
(3)观察函数的图象,回答下列问题: ①图象与x轴有个交点,所以对应的方程2+ ![]() =0实数根是;
=0实数根是;
②函数图象的对称性是 .
A、既是轴对称图形,又是中心对称图形
B、只是轴对称图形,不是中心对称图形
C、不是轴对称图形,而是中心对称图形
D、既不是轴对称图形也不是中心对称图形
(4)写出函数y=2+ ![]() 与y=
与y= ![]() 的图象之间有什么关系?(从形状和位置方面说明)
的图象之间有什么关系?(从形状和位置方面说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=6,那么点B与C′的距离为( ) 
A.3
B.3 ![]()
C.3 ![]()
D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com