
 x2+bx+c经过点A(0,1)、B(3,
x2+bx+c经过点A(0,1)、B(3, )两点,BC⊥x轴,垂足为C.点P是线段AB上的一动点(不与A,B重合),过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t.
)两点,BC⊥x轴,垂足为C.点P是线段AB上的一动点(不与A,B重合),过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t.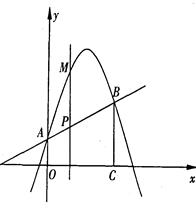
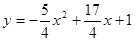 (2)
(2)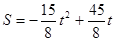 ; 当
; 当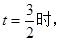

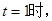 四边形PMBC为菱形。
四边形PMBC为菱形。 x2+bx+c经过点A(0,1)、B(3,
x2+bx+c经过点A(0,1)、B(3, )两点,那么
)两点,那么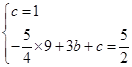 ,解得
,解得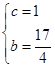 ,所以此抛物线的函数表达式是
,所以此抛物线的函数表达式是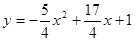
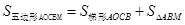 ,而
,而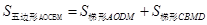 ,
,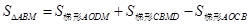 ;M、P点的横坐标相同,由(1)知抛物线的解析式是
;M、P点的横坐标相同,由(1)知抛物线的解析式是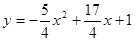 ,所以M的纵坐标为
,所以M的纵坐标为 ;由题知A0=1,BC=
;由题知A0=1,BC=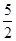 ,OD=t,CD=OC-OD=3-t,DM=
,OD=t,CD=OC-OD=3-t,DM=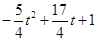 ,所以
,所以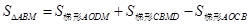 =
=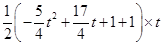 +
+ -
-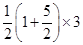 =
=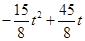 ,
, =
= 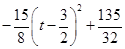 ,要使
,要使 有最大值,那么当且仅当
有最大值,那么当且仅当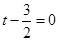 ,即当
,即当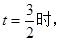

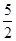 ,PM=PC=BC=
,PM=PC=BC=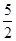 ,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t,M的纵坐标为
,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t,M的纵坐标为 ,MD=
,MD=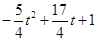 ,PD=MD-MP=
,PD=MD-MP=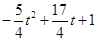 -
-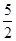 =
=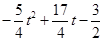 ,在
,在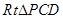 中,由勾股定理得
中,由勾股定理得 ,即
,即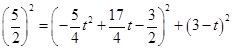 ,解得
,解得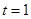 ,所以
,所以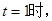 四边形PMBC为菱形
四边形PMBC为菱形

 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源:不详 题型:解答题
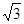 ),点D的坐标为(1,
),点D的坐标为(1,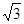 ),点C在
),点C在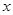 轴的正半轴上,过点O且以点D为顶点的抛物线经过点C,点P为CD的中点.
轴的正半轴上,过点O且以点D为顶点的抛物线经过点C,点P为CD的中点.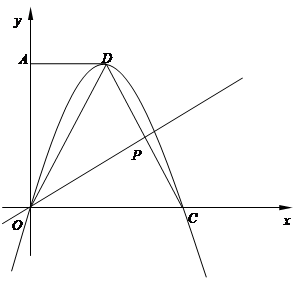
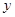 轴右侧的抛物线上是否存在点Q,使以Q为圆心的圆同时与
轴右侧的抛物线上是否存在点Q,使以Q为圆心的圆同时与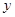 轴、直线OP相切.若存在,请求出满足条件的点Q的坐标;若不存在,请说明理由;
轴、直线OP相切.若存在,请求出满足条件的点Q的坐标;若不存在,请说明理由;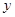 轴的正半轴交于点N.求证:OM+ON为定值.
轴的正半轴交于点N.求证:OM+ON为定值.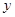 轴上找一点H,使∠PHD最大.试求出点H的坐标.
轴上找一点H,使∠PHD最大.试求出点H的坐标.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y=(x-2) 2+1 | B.y=(x-2) 2-1 |
| C.y=(x+2) 2+1 | D.y=(x+2) 2-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com