
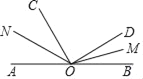
【题目】如图,点O是直线AB上一点,OC⊥OD,OM是∠BOD的角平分线,ON是∠AOC的角平分线,则∠MON的度数是_____°.
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 经过点
经过点![]() (9,10),交
(9,10),交![]() 轴于点
轴于点![]() ,直线
,直线![]() ∥
∥![]() 轴,点
轴,点![]() 是直线
是直线![]() 下方抛物线上的动点.
下方抛物线上的动点.
(1)直接写出抛物线的解析式为 ,点![]() 的坐标为 、
的坐标为 、![]() 的坐标为 _;
的坐标为 _;
(2)过点![]() 且与
且与![]() 轴平行的直线
轴平行的直线![]() 与直线
与直线![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,当四边形
,当四边形![]() 的面积最大时,求
的面积最大时,求![]() 点的坐标;
点的坐标;
(3)如图2,当点![]() 为抛物线的顶点时,在直线
为抛物线的顶点时,在直线![]() 上是否存在点
上是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,若存在,求出点
相似,若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在七年级的一次“数学联欢会”上,数学老师李老师出示了10张数学答题卡,答题卡背面的图案不同:当答题卡正面是正数时,背面是一面五星红旗;当答题卡的正面是负数时,背面是一朵牡丹花。这10张答题卡如图所示:

请你指出这10张答题卡后面有几面五星红旗?有几朵牡丹花?并写出它们的卡片号码。
查看答案和解析>>
科目:初中数学 来源: 题型:
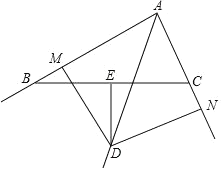
【题目】如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于M,DN⊥AC的延长线于N.
(1)求证:BM=CN;
(2)若AB=8,AC=4,求BM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG,AH=CF.

(1)求证:四边形EFGH是平行四边形;
(2)如果AB=AD,且AH=AE,求证:四边形EFGH是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
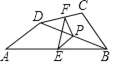
【题目】如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,且∠A+∠ABC=90°,则∠PEF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() ,点
,点![]() 、
、![]() 在直线
在直线![]() 上,点
上,点![]() 、
、![]() 在直线
在直线![]() 上,点
上,点![]() 在点
在点![]() 的右侧,
的右侧,![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,直线
,直线![]() 、
、![]() 交于点
交于点![]() .
.

(1)写出![]() 的度数 ;
的度数 ;
(2)试求![]() 的度数(用含n的代数式表示);
的度数(用含n的代数式表示);
(3)将线段![]() 向右平行移动,使点
向右平行移动,使点![]() 在点
在点![]() 的右侧,其他条件不变,请画出图形并直接写出
的右侧,其他条件不变,请画出图形并直接写出![]() 的度数(用含n的代数式表示).
的度数(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚相约周末到净月潭国家森林公园去徒步,小明和小刚的家分别距离公园1600米和2800米,两人分别从家中同时出发,小明骑自行车,小刚乘公交车,已知公交车的平均速度是骑自行车速度的3.5倍,结果小刚比小明提前4min到达公园,求小刚乘公交车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
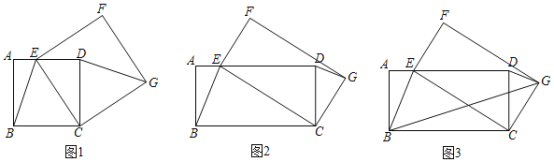
【题目】(问题情境)(1)如图1,四边形ABCD是正方形,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE,则DG与BE的数量关系是 ;
(类比探究)
(2)如图2,四边形ABCD是矩形,AB=2,BC=4,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE.判断线段DG与BE有怎样的数量关系和位置关系,并说明理由;
(拓展提升)
(3)如图3,在(2)的条件下,连接BG,则2BG+BE的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com