
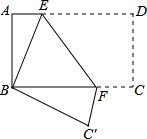
 如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )
如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
分析 由折叠特性可得CD=BC′=AB,∠FC′B=∠EAB=90°,∠EBC′=∠ABC=90°,推出∠ABE=∠C′BF,所以△BAE≌△BC′F,根据△ABE和△BC′F的周长=2△ABE的周长求解.
解答 解:将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,
由折叠特性可得,CD=BC′=AB,∠FC′B=∠EAB=90°,∠EBC′=∠ABC=90°,
∵∠ABE+∠EBF=∠C′BF+∠EBF=90°
∴∠ABE=∠C′BF
在△BAE和△BC′F中,
$\left\{\begin{array}{l}{∠FC′B=∠EAB}\\{BC′=AB}\\{∠ABE=∠C′BF}\end{array}\right.$,
∴△BAE≌△BC′F(ASA),
∵△ABE的周长=AB+AE+EB=AB+AE+ED=AB+AD=1+2=3,
△ABE和△BC′F的周长=2△ABE的周长=2×3=6.
点评 本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,折叠前后图形的形状和大小不变,如本题中折叠前后角边相等.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:选择题
 如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( )
如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 以正方形ABCD的对角线AC、BD所在直线为坐标轴,建立平面直角坐标系,如图所示,已知点A的坐标是(-$\sqrt{2}$,0),现将正方形ABCD绕原点O顺时针旋转45°,则旋转后点C的对应点坐标是( )
以正方形ABCD的对角线AC、BD所在直线为坐标轴,建立平面直角坐标系,如图所示,已知点A的坐标是(-$\sqrt{2}$,0),现将正方形ABCD绕原点O顺时针旋转45°,则旋转后点C的对应点坐标是( )| A. | ($\sqrt{2}$,$\sqrt{2}$) | B. | ($\sqrt{2}$,-$\sqrt{2}$) | C. | (-1,1) | D. | (1,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
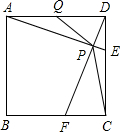 在边长为2cm的正方形ABCD中,动点E、F分别从D、C两点同时出发,都以1cm/s的速度在射线DC、CB上移动.连接AE和DF交于点P,点Q为AD的中点.若以A、P、Q为顶点的三角形与以P、D、C为顶点的三角形相似,则运动时间t为2或4秒.
在边长为2cm的正方形ABCD中,动点E、F分别从D、C两点同时出发,都以1cm/s的速度在射线DC、CB上移动.连接AE和DF交于点P,点Q为AD的中点.若以A、P、Q为顶点的三角形与以P、D、C为顶点的三角形相似,则运动时间t为2或4秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y1<y2 | D. | y3<y2<y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com