

分析 (1)如图1中,延长AD交⊙O于点M,连接MC.首先证明∠ACM=90°,再证明∠ABC=∠M即可解决问题.
(2)如图2中,过点O作OH⊥AC于H,连接BO.想办法证明△BDE≌△AOH即可解决问题.
(3)如图3中,过点O作ON⊥EG于N,OT⊥AB于T,连接OG.由△BFE≌△OFN,推出BE=ON EF=FN由OF=OD,ON⊥FD,推出EF=FN=ND=$\sqrt{15}$,由△BED≌△NOG,推出ED=NG,再证明AE=3BE,设AO=BD=r,OD=$\frac{1}{2}$r,AD=$\frac{3}{2}$r在Rt△AED中,AE2=AD2-ED2,在Rt△BED中,BE2=BD2-ED2,即($\frac{3}{2}$r)2-(3$\sqrt{15}$)2=9[($\frac{1}{2}$r)2-(3$\sqrt{15}$)2],求出r即可解决问题.
解答 (1)证明:如图1中,延长AD交⊙O于点M,连接MC.
∵AM为⊙O的直径,
∴∠ACM=90°,
∴∠ABC=∠AMC,
∵∠AMC+∠MAC=90°,
∴∠B+∠CAD=90°.
(2)证明:如图2中,过点O作OH⊥AC于H,连接BO.
∴∠AOB=2∠ACB,
∵∠ADC=2∠ACB,
∴∠AOB=∠ADC,
∴∠BOD=∠BDO,
∴BD=BO,
∵∠BED=∠AHO,∠ABD=∠AOH,
∴△BDE≌△AOH,
∴DE=AH,
∵OH⊥AC,
∴AH=CH=$\frac{1}{2}$AC,
∴AC=2DE.
(3)证明:如图3中,过点O作ON⊥EG于N,OT⊥AB于T,连接OG.
∵AC=6$\sqrt{15}$,AC=2DE,
∴DE=3$\sqrt{15}$,
∵OA=OB,
∴∠ABO=∠BAO,
∵∠ABO+∠BFE=90°,∠BAO+∠ADE=90°,
∴∠BFE=∠OFD=∠ODF,
∴OF=OD,
∵BF=OD,
∴OF=OD=BF,
∴△BFE≌△OFN,
∴BE=ON EF=FN
∵OF=OD,ON⊥FD,
∴EF=FN=ND=$\sqrt{15}$,
∵BE=ON,OG=BD,
∴△BED≌△NOG,
∴ED=NG,
∴EG=5$\sqrt{15}$,
∵ON⊥EG OT⊥AB DE⊥AB,
∴四边形ONET为矩形,
∴BE=ET=ON,
∵OT⊥AB,
∴AT=BT,AE=3BE,
设AO=BD=r,OD=$\frac{1}{2}$r,AD=$\frac{3}{2}$r
在Rt△AED中,AE2=AD2-ED2,
在Rt△BED中,BE2=BD2-ED2,
即($\frac{3}{2}$r)2-(3$\sqrt{15}$)2=9[r2-(3$\sqrt{15}$)2],
r=4$\sqrt{10}$ 或r=-4$\sqrt{10}$ (舍去),
∴AE=15,
在△AEG中,AG=$\sqrt{A{E}^{2}+E{G}^{2}}$=10$\sqrt{6}$.
点评 本题考查圆综合题、垂径定理、直径的性质、全等三角形的判定和性质、矩形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用构建方程的思想思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
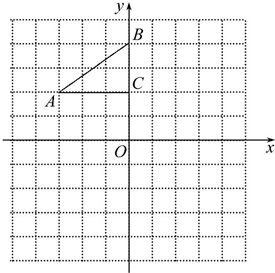 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
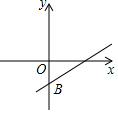 如图是一次函数y=kx+b的图象的大致位置,试判断关于x的一元二次方程x2-2x+kb+1=0的根的判别式△>0(填:“>”或“=”或“<”).
如图是一次函数y=kx+b的图象的大致位置,试判断关于x的一元二次方程x2-2x+kb+1=0的根的判别式△>0(填:“>”或“=”或“<”).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com