练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．如图，菱形ABCD中，E、F分别是AB、AC的中点，若EF=3，求菱形ABCD的周长．

    分析 先根据三角形中位线定理得到BC=2EF=6，然后根据菱形的性质计算菱形ABCD的周长．

    解答 解：∵E、F分别是AB、AC的中点，
    ∴EF为△ABC的中位线，
    ∴BC=2EF=6，
    ∵四边形ABCD为菱形，
    ∴BC=CD=AD=AB=6，
    ∴菱形ABCD的周长=4×6=24．

    点评 本题考查了菱形的性质：菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角．也考查了三角形的中位线定理．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

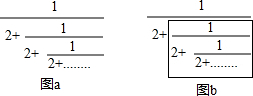    13．观察图a所示算式，该算式由无数层分数线及相同的加数2循环嵌套而成，由图b我们发现，因为有无数层分数线嵌套，因此方框内的部分与整个算式相同，我们假设算式的结果为x，那么就可以将该算式转化成$\frac{1}{2+x}$，从而得到方程$\frac{1}{2+x}$=x．求解出该算式的结果
    问题：如果x=$\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{…}}}}$，y=$\sqrt{2\sqrt{2\sqrt{2\sqrt{…}}}}$，请用上面的方法比较x与y的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．观察下面的一列数：+1，+2，-3，-4，+5，+6，-7，-8，…
    （1）这列数是按照什么规律写出来的？
    （2）这列数的前200个数的和是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．计算与化简下面的二次根式
    （1）2$\sqrt{12}$-$\sqrt{27}$
    （2）（3$\sqrt{5}$-1）2
    （3）2$\sqrt{12}$×$\frac{\sqrt{3}}{4}$÷5$\sqrt{2}$
    （4）（$\sqrt{24}$-$\sqrt{\frac{1}{2}}$）-（$\sqrt{\frac{1}{8}}$+$\sqrt{6}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．在Rt△ABC中，∠ACB=90°，BC=1，AB=2，则sinA=$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

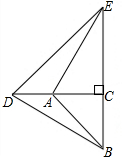    8．如图，△ACB和△DCE都是等腰直角三角形，点A在线段CD上，连接AE、BD．
    （1）求证：AE=BD；
    （2）若AB=CD，将△ACB绕点C逆时针旋转一周，当以A、B、C、D为顶点的四边形是平行四边形时，直接写出旋转角的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．某中学七年级A班有50人，某次活动中分为四组，第一组有a人，第二组比第一组的一半多6人，第三组的人数等于前两组人数的和．
    （1）求第三组的人数．（用含a的式子表示）
    （2）求第四组的人数．（用含a的式子表示）
    （3）试判断a=2时，是否满足题意．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列事件的概率为$\frac{1}{2}$的有（　　）
    ①从1，2，-3，-4四个数中，随机抽取两个数相乘，积是正数的概率；
    ②抛一枚质地均匀的硬币，第10次抛得正面朝上的概率；
    ③如图1，A、B是数轴上的两点，分别表示数-1、3，在线段AB上任意取一点C，则点C到表示数1的点的距离不大于1的概率；
    ④如图2，一圆盘上画有两个同心圆，由里向外半径为1：2，将圆盘分成两部分，飞镖可落在圆盘上任何一部分内，则飞镖在白色区域的概率．
    A．①②B．①③C．②③D．②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．甲、乙两商场自行定价销售某一商品．
    （1）甲商场将该商品提价15%后的售价为1.15元，则该商品在甲商场的原价为1元；
    （2）乙商场将该商品提价20%后，用6元钱购买该商品的件数比没提价前少买1件，求该商品在乙商场的原价是多少？

    查看答案和解析>>

    同步练习册答案