
【题目】“六一”儿童节前,某玩具商店根据市场调查,用2500元购进一批儿童玩具,上市后很快脱销,接着又用4500元购进第二批这种玩具,所购数量是第一批数量的1.5倍,但每套进价多了10元.
(1)求第一批玩具每套的进价是多少元?
(2)如果这两批玩具每套售价相同,且全部售完后总利润不低于25%,那么每套售价至少是多少元?
【答案】
(1)解:设第一批玩具每套的进价是x元,
![]() ×1.5=
×1.5= ![]() ,
,
x=50,
经检验x=50是分式方程的解,符合题意.
答:第一批玩具每套的进价是50元
(2)解:设每套售价是y元,
![]() ×1.5=75(套).
×1.5=75(套).
50y+75y﹣2500﹣4500≥(2500+4500)×25%,
y≥70,
答:如果这两批玩具每套售价相同,且全部售完后总利润不低于25%,那么每套售价至少是70元
【解析】(1)设第一批玩具每套的进价是x元,则第一批进的件数是: ![]() ,第二批进的件数是:
,第二批进的件数是: ![]() ,再根据等量关系:第二批进的件数=第一批进的件数×1.5可得方程;(2)设每套售价是y元,利润=售价﹣进价,根据这两批玩具每套售价相同,且全部售完后总利润不低于25%,可列不等式求解.
,再根据等量关系:第二批进的件数=第一批进的件数×1.5可得方程;(2)设每套售价是y元,利润=售价﹣进价,根据这两批玩具每套售价相同,且全部售完后总利润不低于25%,可列不等式求解.
【考点精析】关于本题考查的分式方程的应用,需要了解列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位)才能得出正确答案.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】已知:m,x,y满足:(1)![]() ;(2)﹣2a2by+1与7b3a2是同类项.
;(2)﹣2a2by+1与7b3a2是同类项.
求代数式:2x2﹣6y2+m(xy﹣9y2)﹣(3x2﹣3xy+7y2)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
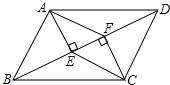
【题目】如图,在□ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F,试判断:
(1)△ABE和△CDF全等吗?请说明理由;
(2)四边形AECF是不是平行四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将自然数按如表规律排列,表中数2在第二行第一列,与有序数对![]() 对应,数5与
对应,数5与![]() 对应,数14与
对应,数14与![]() 对应,根据这一规律,数2014对应的有序数对为__________.
对应,根据这一规律,数2014对应的有序数对为__________.
第一列 | 第二列 | 第三列 | 第四列 | 第五列 | ||
第一行 | 1 | 4 | 5 | 16 | 17 | … |
第二行 | 2 | 3 | 6 | 15 | … | |
第三行 | 9 | 8 | 7 | 14 | … | |
第四行 | 10 | 11 | 12 | 13 | … | |
第五行 | … | |||||
…… |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将自然数按如表规律排列,表中数2在第二行第一列,与有序数对![]() 对应,数5与
对应,数5与![]() 对应,数14与
对应,数14与![]() 对应,根据这一规律,数2014对应的有序数对为__________.
对应,根据这一规律,数2014对应的有序数对为__________.
第一列 | 第二列 | 第三列 | 第四列 | 第五列 | ||
第一行 | 1 | 4 | 5 | 16 | 17 | … |
第二行 | 2 | 3 | 6 | 15 | … | |
第三行 | 9 | 8 | 7 | 14 | … | |
第四行 | 10 | 11 | 12 | 13 | … | |
第五行 | … | |||||
…… |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3(a≠0)经过A(3,0),B(4,1)两点,且与y轴交于点C.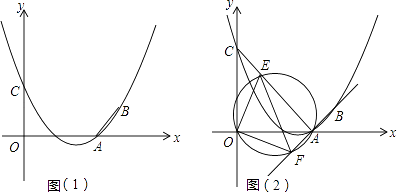
(1)求抛物线y=ax2+bx+3(a≠0)的函数关系式及点C的坐标;
(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=30°,点D在BC边上,点E在AC边上,AD=BD,DE=CE,若△ADE为等腰三角形,则∠C的度数为( )
A. 20° B. 20°或30° C. 30°或40° D. 20°或40°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com