
 ,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOC=∠COB=BOA=120°,按下列要求画图(保留画图痕迹):
,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOC=∠COB=BOA=120°,按下列要求画图(保留画图痕迹):
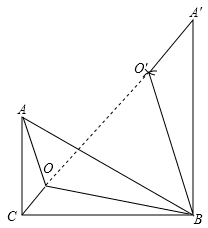
 。
。 ,∴
,∴ 。∴∠ABC=30°。
。∴∠ABC=30°。 。
。

 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源:不详 题型:解答题
 (0°<
(0°< <90°)角,在旋转过程中,直线DE与AC相交于点M,直线DF与BC相交于点N,分别过点M, N作直线AB的垂线,垂足分别为G, H.
<90°)角,在旋转过程中,直线DE与AC相交于点M,直线DF与BC相交于点N,分别过点M, N作直线AB的垂线,垂足分别为G, H.
 =30°时(如图2),求证:AG=DH;
=30°时(如图2),求证:AG=DH;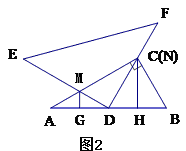
 =60°时(如图3),(1)中的结论是否仍成立?请写出你的结论,并说明理由.
=60°时(如图3),(1)中的结论是否仍成立?请写出你的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
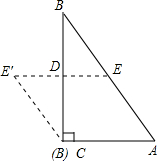
 的位置,若AE=1,BE=2,CE=3,则∠
的位置,若AE=1,BE=2,CE=3,则∠ = 度.
= 度.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
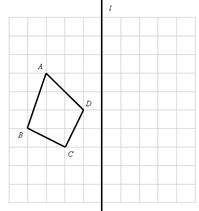
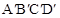 ,使四边形
,使四边形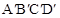 和四边形ABCD关于直线l对称,
和四边形ABCD关于直线l对称,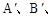
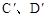 分别是点A、B、C、D的对称点;
分别是点A、B、C、D的对称点; 的长度。
的长度。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com