����⣺��1����y=0����-x-1=0��
���x=-1��
���ԣ���A������Ϊ��-1��0����
�������߽���ʽΪy=ax
2+bx+c��
��B��3��0����C��0��-3�����������ϣ�
��
��
���
��
���ԣ������߽���ʽΪy=x
2-2x-3��
��2����P���߶�AD�ϵ�һ�����㣬��P����y���ƽ���߽���������E�㣬
�����P��x��-x-1�������E��������x��x
2-2x-3����
PE=��-x-1��-��x
2-2x-3����
=-x-1-x
2+2x+3��
=-x
2+x+2��
=-��x-
��
2+
��
����
��
���
��
��
���ԣ���D������Ϊ��2��-3����
��P���߶�AD�ϵ�һ�����㣬
��-1��x��2��
�൱x=
ʱ��PE�����ֵ�����ֵΪ
��
��3����y=x
2-2x-3=��x-1��
2-4��
���F������Ϊ��1��-4������G�ĺ�����Ϊ1��
y=-1-1=-2��
���G��������-1��-2����
��GF=-2-��-4��=-2+4=2��
���ı���GFEPΪƽ���ı��Σ�
��PE=GF��
��-x
2+x+2=2��
���x
1=0��x
2=1����ȥ����
��ʱ��y=-1��
���P��������0��-1����
�ʣ����ڵ�P��0��-1����ʹ���ı���GFEPΪƽ���ı��Σ�
��4�����ڣ��������£�
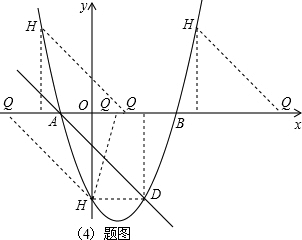
�ٵ���H��x���·�ʱ���ߵ�Q��x���ϣ�
��HD��AQ��
���H�����������D��ͬ����-3��
��ʱ��x
2-2x-3=-3��
�����ã�x
2-2x=0��
���x
1=0��x
2=2����ȥ����
��HD=2-0=2��
�ߵ�A������Ϊ��-1��0����
-1-2=-3��-1+2=1��
���Q��������-3��0����1��0����
�ڵ���H��x���Ϸ�ʱ������ƽ���ı��εĶԳ��ԣ���H��AQ�ľ�����ڵ�D��AQ�ľ��룬
�ߵ�D��������Ϊ-3��
���H��������Ϊ3��
��x
2-2x-3=3��
�����ã�x
2-2x-6=0��
���x
1=1-
��x
2=1+
��
�ߵ�A�ĺ�����Ϊ-1����D�ĺ�����Ϊ2��
2-��-1��=2+1=3��
����ƽ���ı��ε����ʣ�1-
+3=4-
��1+
+3=4+
��
���Q��������4-
��0����4+
��0����
�������������ڵ�Q��-3��0����1��0����4-
��0����4+
��0����ʹA��D��H��Q���ĸ���Ϊ������ı�����ƽ���ı��Σ�

 ��ͼ��ֱ��AD��Ӧ�ĺ�����ϵʽΪy=-x-1���������߽��ڵ�A����x���ϣ�����D����������x����һ����ΪB��3��0������������y�ύ��C��0��-3����
��ͼ��ֱ��AD��Ӧ�ĺ�����ϵʽΪy=-x-1���������߽��ڵ�A����x���ϣ�����D����������x����һ����ΪB��3��0������������y�ύ��C��0��-3����



 ��֪����ͼ����ABC�У�DE��BC��AD��DB=3��2����S��ADE��S�ı���BCED=��������
��֪����ͼ����ABC�У�DE��BC��AD��DB=3��2����S��ADE��S�ı���BCED=�������� Ϊ��Ԥ�����У�ij��ѧ����ĩ��ҩѬ�������Խ��ҽ�����������֪ҩ���ͷŹ����У�����ÿ���������еĺ�ҩ��y�����ˣ���ʱ��x�����ӣ�����������ҩ���ͷ���Ϻ�y��x�ɷ�����������������y��x��ͼ������ͼ���ݲⶨ����������ÿ�����ĺ�ҩ�����͵�0.45��������ʱ��ѧ�����ɽ�����ң���ô��ҩ���ͷ���Ͽ�ʼ�����辭����������Сʱ��ѧ�����ܽ�����ң�
Ϊ��Ԥ�����У�ij��ѧ����ĩ��ҩѬ�������Խ��ҽ�����������֪ҩ���ͷŹ����У�����ÿ���������еĺ�ҩ��y�����ˣ���ʱ��x�����ӣ�����������ҩ���ͷ���Ϻ�y��x�ɷ�����������������y��x��ͼ������ͼ���ݲⶨ����������ÿ�����ĺ�ҩ�����͵�0.45��������ʱ��ѧ�����ɽ�����ң���ô��ҩ���ͷ���Ͽ�ʼ�����辭����������Сʱ��ѧ�����ܽ�����ң�