
【题目】如图,已知:点B、E、F、C在同一直线上,∠A=∠D,BE=CF,且AB∥CD.求证:AF∥ED
证明:∵BE=FC
∴BE+EF=FC+EF(____________________________)
即:___________
∵AB∥CD
∴∠B=∠C(_________________________)
在△ABF和△DCE中,
∠A=∠D, ∠B=∠C, BF=CE
∴△ABF≌△DCE(________)
∴∠AFB=∠DEC(_________________________________)
∴AF∥ED(__________________________________)

【答案】等式的性质BF=CE两直线平行内错角相等AAS全等三角形对应角相等内错角相等两直线平行
【解析】
由BE= CF,利用等式的性质得到BF= CE ,再由AB与DC平行得到两对内错角相等,利用AAS得到△ABF与△DCE全等,利用全等三角形的对应角相等得到一对内错角相等,利用内错角相等两直线平行即可得证.
证明:∵BE=FC
∴BE+EF=FC+EF( 等式的性质 )
即: BF=CE
∵AB∥CD
∴∠B=∠C( 两直线平行内错角相等 )
∠A=∠D
∠B=∠C
在△ABF和△DCE中,有
BF=CE
∴△ABF≌△DCE( AAS )
∴∠AFB=∠DEC( 全等三角形对应角相等 )
∴AF∥ED( 内错角相等两直线平行 )


科目:初中数学 来源: 题型:
【题目】某中学开展“英语演讲”比赛活动,八年级(1),(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示,

(1)根据图示填写下表:
班级 | 平均数(分) | 中位数(分) | 众数(分) |
八(1) | ______ | 85 | ______ |
八(2) | 85 | ______ | 100 |
(2)计算两班复赛成绩的方差并说明哪版的成绩比较稳定.(方差公式:S2=![]() ])
])
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:菱形 ABCD,点 E 在线段 BC 上,连接 DE,点 F 在线段 AB 上,连接 CF、DF, CF 与 DE 交于点 G,将菱形 ABCD 沿 DF 翻折,点 A 恰好落在点 G 上.
(1)求证:CD=CF;
(2)设∠CED= x,∠DCF= y,求 y 与 x 的函数关系式;(不要求写出自变量的取值范围)
(3)在(2)的条件下,当 x=45°时,以 CD 为底边作等腰△CDK,顶角顶点 K 在菱形 ABCD的内部,连接 GK,若 GK∥CD,CD=4 时,求线段 KG 的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sin B=![]() ,AD=1.
,AD=1.

(1)求BC的长;
(2)求tan ∠DAE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(-2,n)在抛物线y=x2+bx+c上.
(1)若b=1,c=3,求n的值;
(2)若此抛物线经过点B(4,n),且二次函数y=x2+bx+c的最小值是-4,请画出点P(x-1,x2+bx+c)的纵坐标随横坐标变化的图象,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明口袋中装有5个白球和6个红球,这些球除颜色外完全相同,充分搅匀后随机摸球.
(1)如果先摸出一白球,将这个白球放回,再摸出一球,那么它是白球的概率是多少?
(2)如果先摸出一白球,这个白球不放回,再摸出一球,那么它是白球的概率是多少?
(3)如果先摸出一红球,这个红球不放回,再摸出一球,那么它是白球的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年11月11日,张杰参加了某网点的“翻牌抽奖”活动.如图所示,4张牌上分别写有对应奖品的价值为10元,15元,20元和“谢谢惠顾”的字样.
⑴如果随机翻1张牌,那么抽中有奖的概率为 ,抽中15元及以上奖品的概率为 .
⑵如果随机翻2张牌,且第一次翻过的牌不再参加下次翻牌,用画树状图或列表法列出抽奖的所有等可能性情况,并求出获奖品总值不低于30元的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
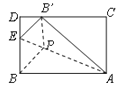
【题目】矩形纸片ABCD中,AB=3,AD=4,将纸片折叠,使点B落在边CD上的B’处,折痕为AE.在折痕AE上存在一点P到边CD的距离与到点B的距离相等,则此相等距离为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )

A. abc<0 B. -3a+c<0
C. b2-4ac≥0 D. 将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com