
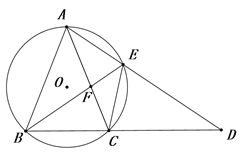
【题目】如图,△ABC内接于⊙O,且AB=AC.延长BC到点D,使CD=CA,连接AD交⊙O于点E.
(1)求证:△ABE≌△CDE;
(2)填空:
①当∠ABC的度数为 时,四边形AOCE是菱形;
②若AE=6,BE=8,则EF的长为 .
【答案】(1)证明见解析(2)①60②![]()
【解析】分析:(1)根据AAS证明两三角形全等;
(2)①先证明∠AOC=∠AEC=120°,∠OAE=∠OCE=60°,可得AOCE,由OA=OC可得结论;
②根据(1)中的全等得:BE=DE=8,AE=CE=6,证明△ECD∽△CFB,列式可得:![]() =
=![]() ,证明△AEF∽△BCF,则可得EF的长.
,证明△AEF∽△BCF,则可得EF的长.
详解:(1)证明:∵AB=AC,CD=CA,∴∠ABC=∠ACB,AB=CD.
∵四边形ABCE是圆内接四边形,∴∠ECD=∠BAE,∠CED=∠ABC.
∵∠ABC=∠ACB=∠AEB,∴∠CED=∠AEB,∴△ABE≌△CDE(AAS);
(2)①当∠ABC的度数为60°时,四边形AOCE是菱形;
理由是:连接AO、OC.
∵四边形ABCE是圆内接四边形,∴∠ABC+∠AEC=180°.
∵∠ABC=60,∴∠AEC=120°=∠AOC.
∵OA=OC,∴∠OAC=∠OCA=30°.
∵AB=AC,∴△ABC是等边三角形,∴∠ACB=60°.
∵∠ACB=∠CAD+∠D.
∵AC=CD,∴∠CAD=∠D=30°,∴∠ACE=180°﹣120°﹣30°=30°,∴∠OAE=∠OCE=60°,∴四边形AOCE是平行四边形.
∵OA=OC,∴AOCE是菱形;
②由(1)得:△ABE≌△CDE,∴BE=DE=8,AE=CE=6,∴∠D=∠EBC.
∵∠CED=∠ABC=∠ACB,∴△ECD∽△CFB,∴![]() =
=![]() .
.
∵∠AFE=∠BFC,∠AEB=∠FCB,∴△AEF∽△BCF,∴![]() =
=![]() ,∴EF=
,∴EF=![]() =
=![]() .
.
故答案为:①60°;②![]() .
.



科目:初中数学 来源: 题型:
【题目】某超市为加快资金回笼,特推出如下优惠方案:
①一次购买价值不超过200元的商品,不享受优惠;
②一次购买价值超过200元,但不超过500元的商品,一律九折;
③一次购买价值超过500元的商品,一律八折.
根据以上方案解决下列问题:
(1)若某人一次购买价值350元的商品,则实际应付款 元(直接填空);
(2)某人一次购买了价值![]() 元的商品,实际付款432元,求
元的商品,实际付款432元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种水果第一天以2元/斤的价格卖出a斤,第二天以1.5元/斤的价格卖出b斤第三天以1.2元/斤的价格卖出c斤,求:
(1)这三天一共卖出水果多少斤?
(2)这三天一共卖得多少钱?
(3)这三天平均售价是多少?并计算当a=30,b=40,c=45时,平均售价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】选取二次三项式![]() 中的两项,配成完全平方式的过程叫作配方.例如①选取二次项和一次项配方:
中的两项,配成完全平方式的过程叫作配方.例如①选取二次项和一次项配方:![]() ;②选取二次项和常数项配方:
;②选取二次项和常数项配方:![]() 或
或![]() ;③选取一次项和常数项配方:
;③选取一次项和常数项配方:![]() .
.
根据上述材料解决下面问题:
(1)写出![]() 的两种不同形式的配方.
的两种不同形式的配方.
(2)已知![]() ,求
,求![]() 的值.
的值.
(3)已知a、b、c为三条线段,且满足![]() ,试判断a、b、c能否围成三角形,并说明理由.
,试判断a、b、c能否围成三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
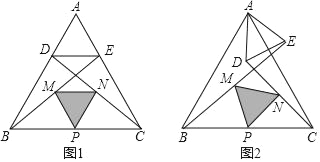
【题目】如图1,在等边△ABC中,点D,E分别在边AB,AC上,AD=AE,连接BE,CD,点M、N、P分别是BE、CD、BC的中点.
(1)观察猜想:图1中,△PMN的形状是 ;
(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,△PMN的形状是否发生改变?并说明理由;
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=1,AB=3,请直接写出△PMN的周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后,分别位于点Q、R处,且相距30海里,如果知道“远航”号沿北偏东![]() 方向航行,请求出“海天”号的航行方向?
方向航行,请求出“海天”号的航行方向?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把 6个相同的小正方体摆成如图的几何体.
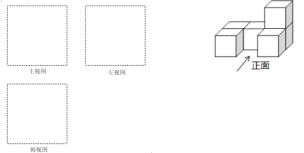
(1)画出该几何体的主视图、左视图、俯视图;
(2)如果每个小正方体棱长为![]() ,则该几何体的表面积是
,则该几何体的表面积是 ![]() .
.
(3)如果在这个几何体上再添加一些相同的小正方体,并并保持左视图和俯视图不变,那么最多可以再 添加 个小正方体.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com