
| A. | ∠A?∠B?∠C=3?4?5 | B. | ∠A:∠B:∠C=1:3:2 | C. | (b+c)(b-c)=a2 | D. | a:b:c=$\frac{3}{2}$?2?$\frac{5}{2}$ |
分析 A、根据比的份数设未知数,根据三角形的内角和列方程求出各角的度数,则可以作判断;
B、利用算术法计算最大角为90°,可以判定此三角形为直角三角形.
C、去括号,根据勾股定理的逆定理,可以判定此三角形为直角三角形;
D、根据勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方,则可以判定此三角形为直角三角形.
解答 解:A、∵∠A?∠B?∠C=5:4:3,
∴设∠A=5x,∠B=4x,∠C=3x,
则5x+4x+3x=180,
12x=180,
x=15,
∴∠A=5x=75°,∠B=4x=60°,∠C=3x=45°,
∴不能判定△ABC是直角三角形,
B、∵∠A:∠B:∠C=1:3:2,
∴∠B=$\frac{3}{1+3+2}$×180°=90°,
∴此条件可以判定△ABC是直角三角形,
C、∵(b+c)(b-c)=a2,
b2-c2=a2,
∴b2=a2+c2,
∴此条件可以判定△ABC是直角三角形,
D、∵a:b:c=$\frac{3}{2}$:2:$\frac{5}{2}$,
设a=$\frac{3}{2}$k,b=2k,c=$\frac{5}{2}$k,
∵$\frac{3}{2}$k<2k<$\frac{5}{2}$k,
$(\frac{3}{2}k)^{2}+(2k)^{2}$=$(\frac{5}{2}k)^{2}$,
∴此条件可以判定△ABC是直角三角形,
因为本题是选择不能判定△ABC为直角三角形的条件,
故选A.
点评 本题考查了三角形的内角和定理和勾股定理和逆定理,知道三角形三个角的比,即可利用方程或算术法求各角的度数,同时要熟练掌握除了计算三角形角的度数来判断一个三角形是不是直角三角形外,还要掌握另一方法:满足较小两边平方的和等于最大边的平方,这样的三角形也是直角三角形.


科目:初中数学 来源: 题型:解答题
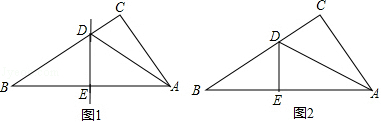
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{12}{5}$ | C. | $\frac{5}{13}$ | D. | $\frac{12}{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com