
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CECA. 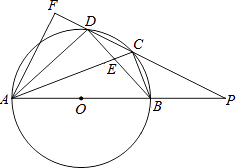
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,过点A作AF⊥CD交CD的延长线于点F,若PB=OB,CD= ![]() ,求DF的长.
,求DF的长.
【答案】
(1)证明:∵DC2=CECA,
∴ ![]() =
= ![]() ,
,
△CDE∽△CAD,
∴∠CDB=∠DAC,
∵四边形ABCD内接于⊙O,
∴BC=CD;
(2)解:方法一:如图,连接OC,
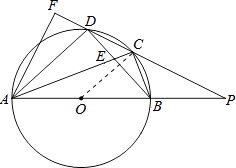
∵BC=CD,
∴∠DAC=∠CAB,
又∵AO=CO,
∴∠CAB=∠ACO,
∴∠DAC=∠ACO,
∴AD∥OC,
∴ ![]() =
= ![]() ,
,
∵PB=OB,CD= ![]() ,
,
∴ ![]() =
= ![]()
∴PC=4 ![]()
又∵PCPD=PBPA
∴4 ![]() (4
(4 ![]() +2
+2 ![]() )=OB3OB
)=OB3OB
∴OB=4,即AB=2OB=8,PA=3OB=12,
在Rt△ACB中,
AC= ![]() =
= ![]() =2
=2 ![]() ,
,
∵AB是直径,
∴∠ADB=∠ACB=90°
∴∠FDA+∠BDC=90°
∠CBA+∠CAB=90°
∵∠BDC=∠CAB,
∴∠FDA=∠CBA,
又∵∠AFD=∠ACB=90°,
∴△AFD∽△ACB
∴ ![]()
在Rt△AFP中,设FD=x,则AF= ![]() ,
,
∴在Rt△APF中有, ![]() ,
,
求得DF= ![]() .
.
方法二;连接OC,过点O作OG垂直于CD,

易证△PCO∽△PDA,可得 ![]() =
= ![]() ,
,
△PGO∽△PFA,可得 ![]() =
= ![]() ,
,
可得, ![]() =
= ![]() ,由方法一中PC=4
,由方法一中PC=4 ![]() 代入
代入 ![]() ,
,
即可得出DF= ![]()
【解析】(1)求出△CDE∽△CAD,∠CDB=∠DAC得出结论.(2)连接OC,先证AD∥OC,由平行线分线段成比例性质定理求得PC= ![]() ,再由割线定理PCPD=PBPA求得半径为4,根据勾股定理求得AC=
,再由割线定理PCPD=PBPA求得半径为4,根据勾股定理求得AC= ![]() ,再证明△AFD∽△ACB,得
,再证明△AFD∽△ACB,得 ![]() ,则可设FD=x,AF=
,则可设FD=x,AF= ![]() ,在Rt△AFP中,利用勾股定理列出关于x的方程,求解得DF.
,在Rt△AFP中,利用勾股定理列出关于x的方程,求解得DF.
【考点精析】根据题目的已知条件,利用勾股定理的概念和圆周角定理的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上
(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;
(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
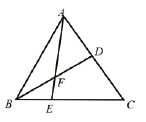
【题目】如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为![]() 且
且![]() =24,则
=24,则![]() =___________
=___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2017年十堰市初中体育中考中,随意抽取某校5位同学跳远的记录分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A.平均数为160
B.中位数为158
C.众数为158
D.方差为20.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x=y,则下列各式①x﹣3=y﹣3,②4x=6y,③﹣2x=﹣2y,④![]() ,⑤
,⑤![]() ,⑥
,⑥![]() ,其中正确的有( )
,其中正确的有( )
A. ①②③ B. ④⑤⑥ C. ①③⑤ D. ②④⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中。

(1)请写出△ABC各点的坐标;
(2)求出△ABC的面积S△ABC;
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A1B1C1,在图中画出△A1B1C1,并写出△A1B1C1的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com