
【题目】计算:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() ;
;
(5)![]() ;
;
(6)![]() ;
;
(7)![]() ;
;
(8)![]() ;
;
(9)![]() ;
;
(10)![]() ;
;
(11)20032;
(12)![]() ;
;
(13)![]() ;
;
(14)![]() ;
;
(15)![]() .
.
【答案】(1)y2m+1(2)16x4y12z8(3)9000000(4)10x315x2+20x(5)256a8-32 a4b4+ b8(6)x+3(7)![]() (8)
(8)![]() (9)
(9)![]() (10)1(11)4012009(12)
(10)1(11)4012009(12)![]() (13)
(13)![]() (14)
(14)![]() (15)37
(15)37
【解析】
(1)直接根据同底数幂的乘法法则计算即可;
(2)直接根据积的乘方法则计算即可;
(3)直接根据积的乘方法则计算即可;
(4)根据整式的乘法法则计算即可;
(5)利用完全平方公式和平方差公式计算;
(6)先将中括号内的因式展开,再合并同类项,最后除以x;
(7)按按照实数的运算法则运算即可;
(8)利用完全平方公式和平方差公式计算;
(9)利用完全平方公式和平方差公式计算;
(10)利用平方差公式计算;
(11)根据完全平方公式进行计算;
(12)根据整式的加减运算法则即可求解;
(13)根据整式的乘除运算法则即可求解;
(14)根据整式的乘除混合运算法则即可求解;
(15)根据负指数幂及零指数幂的运算法则即可求解.
(1)原式=y2m+1
(2)原式=16x4y12z8
(3)原式=9×106=9000000
(4)原式=10x315x2+20x
(5)原式=[(2ab)(4a2+b2)(2a+b)]2,
=[(2ab)(2a+b)(4a2+b2)]2,
=[(4a2b2)(4a2+b2)]2,
=(16a4b4)2
=256a8-32 a4b4+ b8
(6)原式=(x2+3x+22)÷x,
=(x2+3x)÷x,
=x+3
(7)原式=1×2÷![]() ×
×![]()
=2×2×![]() =
=![]()
(8)![]()
=![]()
=![]()
=![]()
(9)![]()
=![]()
=![]()
=![]()
(10)![]()
=![]()
=![]()
=1
(11)20032
=(2000+3)2
=4000000+12000+9
=4012009
(12)![]()
=![]()
=![]()
(13)![]() =
=![]()
(14)![]()
=![]()
=![]()
(15)![]()
=![]()
=37.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若AC=24,AB=30,且
MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若AC=24,AB=30,且![]() =216,则△ABD的面积是( )
=216,则△ABD的面积是( )
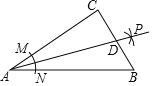
A.105B.120
C.135D.115
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,BD、CE、DE有什么数量关系?并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
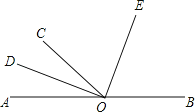
【题目】如图,点O为直线AB上一点,∠AOC=48°,OD平分∠AOC,OE⊥OD交于点O.
(1)求出∠BOD的度数;
(2)试用计算说明∠COE=∠BOE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD,∠ADC的平分线DE,交BC于点E.
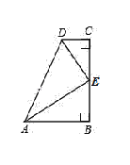
证明:①EC=EB;②AE⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD=BC=12,AB=CD,BD=15,点E从D点出发,以每秒4个单位的速度沿D→A→D匀速移动,点F从点C出发,以每秒1个单位的速度沿CB向点B作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.

(1)试说明:AD∥BC;
(2)在移动过程中,小明发现有△DEG与△BFG全等的情况出现,请你探究这样的情况会出现几次?并分别求出此时的移动时间t和G点的移动距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
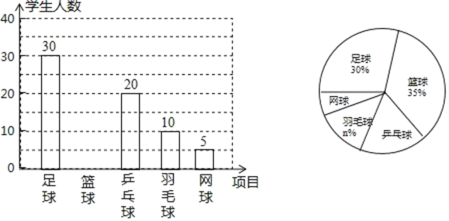
【题目】深圳高级中学(集团)开展“阳光体育活动”,共开设足球,蓝球,乒乓球,羽毛球,网球五项活动,为了了解学生对这五项活动的喜爱情况,随机调查了m名学生(每名学生必须且只能选择这五项运动中的一种),并根据调查的结果绘制了如图所示不完整的统计图.根据以上统计图提供的信息,解答下列问题:
(1)m= ,n= ;
(2)补全条形统计图;
(3)若深高(集团)共有学生6000人,则喜欢乒乓球的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点。
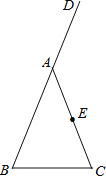
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法)。
①作∠DAC的平分线AM。②连接BE并延长交AM于点F。
(2)猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com