
【题目】为加快“智慧校园”建设,某县准备为试点学校采购一批 ![]() 、
、![]() 两种型号的一体机.经过市场调查发现,今年每套
两种型号的一体机.经过市场调查发现,今年每套 ![]() 型一体机的价格比每套
型一体机的价格比每套 ![]() 型一体机的价格多
型一体机的价格多 ![]() 万元,且用
万元,且用![]() 万元恰好能购买
万元恰好能购买 ![]() 套
套 ![]() 型一体机和
型一体机和 ![]() 套
套 ![]() 型一体机.
型一体机.
(1)求今年每套 ![]() 型、
型、![]() 型一体机的价格各是多少万元?
型一体机的价格各是多少万元?
(2)该县明年计划采购 ![]() 型、
型、![]() 型一体机共
型一体机共 ![]() 套,需投入资金
套,需投入资金 ![]() 万元. 考虑物价因素,预计明年每套
万元. 考虑物价因素,预计明年每套 ![]() 型一体机的价格不变,每套
型一体机的价格不变,每套 ![]() 型一体机的价格比今年上涨
型一体机的价格比今年上涨 ![]() , 设该市明年购买
, 设该市明年购买 ![]() 型一体机
型一体机 ![]() 套.
套.
①请写出该县明年需投入资金 ![]() (万元)与购买
(万元)与购买 ![]() 型一体机
型一体机 ![]() (套)之间的函数关系式 ;
(套)之间的函数关系式 ;
②若该县明年购买 ![]() 型一体机的总费用不低于购买
型一体机的总费用不低于购买 ![]() 型一体机的总费用,那么该县明年至少需要投入多少万元才能完成采购计划?
型一体机的总费用,那么该县明年至少需要投入多少万元才能完成采购计划?
【答案】(1)每套A型一体机的价格为0.8万元,每套B型一体机的价格为0.5万元;(2)①W=﹣0.2m+224,②192
【解析】
(1)直接利用每套 ![]() 型一体机的价格比每套
型一体机的价格比每套 ![]() 型一体机的价格多
型一体机的价格多 ![]() 万元,且用
万元,且用![]() 万元恰好能购买
万元恰好能购买 ![]() 套
套 ![]() 型一体机和
型一体机和 ![]() 套
套 ![]() 型一体机,分别得出方程求出答案;
型一体机,分别得出方程求出答案;
(2)根据题意表示出总费用进而利用一次函数增减性得出答案.
解:(1)设今年每套A型一体机的价格为![]() 万元,每套B型一体机的价格为
万元,每套B型一体机的价格为![]() 万元,
万元,
由题意可得:![]() ,
,
解得:![]() ,
,
(2)①W=0.8(280﹣m)+0.5×(1+20%)m
=﹣0.2m+224,
②由题意可得:0.8(280﹣m)≥0.5(1+20%)m,
解得:m≤160,
在W=﹣0.2m+224中,
∵﹣0.2<0,∴W随m的增大而减小,
∵m≤160,
∴当m=160时,
W有最小值﹣0.2×160+224=192(万元),
故该市明年至少需投入192万元才能完成采购计划.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
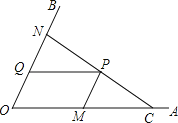
(1)若∠AOB=45°,OM=4,OQ=![]() ,求证:CN⊥OB;
,求证:CN⊥OB;
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问:![]() 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由;
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由;
②设菱形OMPQ的面积为S1,△NOC的面积为S2,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
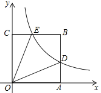
【题目】平面直角坐标系中,正方形OABC如图放置,反比例函数![]() 的图像交AB于点D,交BC于点E,已知A(
的图像交AB于点D,交BC于点E,已知A(![]() ,0),∠DOE=30°,则k的值为( )
,0),∠DOE=30°,则k的值为( )
A.![]() B.
B.![]() C.3D.3
C.3D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
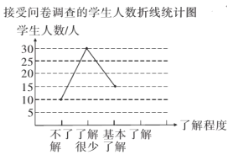
【题目】我校准备近期做一个关于新冠肺炎的专刊学生手抄报,想知道同学们对新冠肺炎知识的了解程度,决定随机抽取部分同学进行次问卷调查,并根据收集到的信息进行了统计,绘制了下面两.幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的同学共有 名;
(2)请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小;
(3)为了让全校师生都能更好地预防新冠肺炎,学生会准备组织一次宣讲活动,由问卷调查中“了解”的几名同学组成一个宣讲团,已知这几名同学中只有两个女生,若要在该宣讲团中任选两名同学在全校师生大会上作代表发言,请用列表或画树状图的方法,求选取的两名同学都是女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P( x, y1)与Q (x, y2)分别是两个函数图象C1与C2上的任一点. 当a ≤ x ≤ b时,有-1 ≤ y1 - y2 ≤ 1成立,则称这两个函数在a ≤ x ≤ b上是“相邻函数”,否则称它们在a ≤ x ≤ b上是“非相邻函数”.
例如,点P(x, y1)与Q (x, y2)分别是两个函数y = 3x+1与y = 2x - 1图象上的任一点,当-3 ≤ x ≤ -1时,y1 - y2 = (3x + 1) - (2x - 1) = x + 2,通过构造函数y = x + 2,并研究它在-3 ≤ x ≤ -1上的性质,得到该函数值的范围是-1 ≤ y ≤ 1,所以-1 ≤ y1 - y2 ≤ 1成立,因此这两个函数在-3 ≤ x ≤ -1上是“相邻函数”.
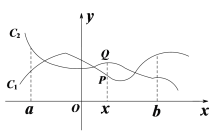
(1)判断函数y = 3x + 2与y = 2x + 1在-2 ≤ x≤ 0上是否为“相邻函数”,并说明理由;
(2)若函数y = x2 - x与y = x - a在0 ≤ x ≤ 2上是“相邻函数”,求a的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山东省济宁市)如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=![]() ,反比例函数
,反比例函数![]() 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )

A. 60B. 80C. 30D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,已知轮船甲在A处沿北偏东65°的方向匀速航行,同时轮船乙在轮船甲的南偏东40°方向的点B处沿某一方向航行,速度与甲轮船的速度相同.若经过一段时间后,两艘轮船恰好相遇,则轮船乙的航行方向为( )
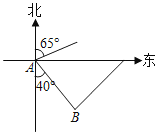
A.北偏西40°B.北偏东40°C.北偏西35°D.北偏东35°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬遵义红色文化,传承红色文化精神,某校准备组织学生开展研学活动.经了解,有A.遵义会议会址、B.苟坝会议会址、C.娄山关红军战斗遗址、D.四渡赤水纪念馆共四个可选择的研学基地.现随机抽取部分学生对基地的选择进行调查,每人必须且只能选择一个基地.根据调查结果绘制如下不完整的条形统计图和扇形统计图.
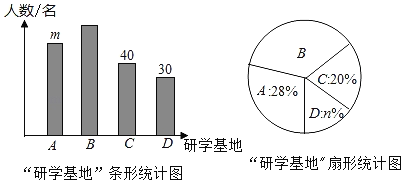
(1)统计图中m= ,n= ;
(2)若该校有1500名学生,请估计选择B基地的学生人数;
(3)某班在选择B基地的4名学生中有2名男同学和2名女同学,需从中随机选出2名同学担任“小导游”,请用树状图或列举法求这2名同学恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“精准扶贫”,某村在政府的扶持下建起了蔬菜大棚基地,准备种植A,B两种蔬菜,若种植20亩A种蔬菜和30亩B种蔬菜,共需投入36万元;若种植30亩A种蔬菜和20亩B种蔬菜,共需投入34万元.
(1)种植A,B两种蔬菜,每亩各需投入多少万元?
(2)经测算,种植A种蔬菜每亩可获利0.8万元,种植B种蔬菜每亩可获利1.2万元,村里把100万元扶贫款全部用来种植这两种蔬菜,总获利w万元.设种植A种蔬菜m亩,求w关于m的函数关系式;
(3)在(2)的条件下,若要求A种蔬菜的种植面积不能少于B种蔬菜种植面积的2倍,请你设计出总获利最大的种植方案,并求出最大总获利.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com