
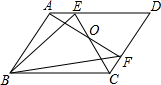
 如图,在?ABCD中.E,F分别是AD,CD上,AF与CE交于点O,有下列命题:
如图,在?ABCD中.E,F分别是AD,CD上,AF与CE交于点O,有下列命题:分析 根据三角形面积公式和平行四边形的面积公式易得S△ABF=S△BEC=$\frac{1}{2}$S平行四边形ABCD,则可对①②解析判断;过点B作BM⊥AF于M,BN⊥CE于N,如图,利用三角形面积公式得S△ABF=$\frac{1}{2}$AF•BM,S△BEC=$\frac{1}{2}$CE•BN,若AF=CE,则BM=BN,根据角平分线性质定理的逆定理得到OB平分∠AOC,则可对③解析判断;当∠AOB=∠BOC,根据角平分线性质定理得到BM=CN,然后由S△ABF=$\frac{1}{2}$AF•BM,S△BEC=$\frac{1}{2}$CE•BN可得AF=CE,于是可对④解析判断.
解答  解:∵四边形ABCD为平行四边形,
解:∵四边形ABCD为平行四边形,
∴AB∥CD,
∴S△ABF=$\frac{1}{2}$S平行四边形ABCD,
同样可得S△BEC=$\frac{1}{2}$S平行四边形ABCD,
∴S△ABF=S△BEC,所以①错误,②正确;
过点B作BM⊥AF于M,BN⊥CE于N,如图,
∵S△ABF=$\frac{1}{2}$AF•BM,S△BEC=$\frac{1}{2}$CE•BN,
而S△ABF=S△BEC,AF=CE,
∴BM=BN,
∴OB平分∠AOC,
即∠AOB=∠BOC,所以③正确;
当∠AOB=∠BOC,则BM=CN,
∵S△ABF=$\frac{1}{2}$AF•BM,S△BEC=$\frac{1}{2}$CE•BN,
而S△ABF=S△BEC,
∴AF=CE,所以④正确.
故答案为②③④.
点评 本题考查了平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分;平行四边形的面积等于它的底和这个底上的高的积.也考查了角平分线的性质和三角形面积公式.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系xOy中,点D为直线y=2x上且在第一象限内的任意一点,DA1⊥x轴于点A1,以DA1为边在DA1的右侧作正方形A1B1C1D;直线OC1与边DA1交于点A2,以DA2为边在DA2的右侧作正方形A2B2C2D;直线OC2与边DA1交于点A3,以DA3为边在DA3的右侧作正方形A3B3C3D,…,按这种方式进行下去,则直线OC1对应的函数表达式为y=$\frac{2}{3}$x,直线OC3对应的函数表达式为y=$\frac{14}{15}x$.
如图,在平面直角坐标系xOy中,点D为直线y=2x上且在第一象限内的任意一点,DA1⊥x轴于点A1,以DA1为边在DA1的右侧作正方形A1B1C1D;直线OC1与边DA1交于点A2,以DA2为边在DA2的右侧作正方形A2B2C2D;直线OC2与边DA1交于点A3,以DA3为边在DA3的右侧作正方形A3B3C3D,…,按这种方式进行下去,则直线OC1对应的函数表达式为y=$\frac{2}{3}$x,直线OC3对应的函数表达式为y=$\frac{14}{15}x$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,等边三角形OAB的边长是2$\sqrt{3}$,且OB边落在x轴的正半轴上,点A落在第一象限.将△OAB沿直线y=kx+b折叠,使点A落在x轴上,设点C是点A落在x轴上的对应点.
在平面直角坐标系中,等边三角形OAB的边长是2$\sqrt{3}$,且OB边落在x轴的正半轴上,点A落在第一象限.将△OAB沿直线y=kx+b折叠,使点A落在x轴上,设点C是点A落在x轴上的对应点. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
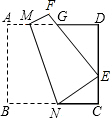 如图,将边长为8的正方形纸片ABCD折叠,使点B落在CD边的中点E上,压平后得到折痕MN,EF与AD边交于点G.
如图,将边长为8的正方形纸片ABCD折叠,使点B落在CD边的中点E上,压平后得到折痕MN,EF与AD边交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
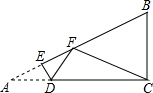 如图,有一直角三角形纸片ACB,∠A=30°,∠ACB=90°,BC=2,点D是AC边上一动点.过点D沿直线DE方向折叠三角形纸片,使点A落在射线AB上的点F处,当以点F、B、C为顶点的三角形为等腰三角形时,AD的长为$\frac{2\sqrt{3}}{3}$.
如图,有一直角三角形纸片ACB,∠A=30°,∠ACB=90°,BC=2,点D是AC边上一动点.过点D沿直线DE方向折叠三角形纸片,使点A落在射线AB上的点F处,当以点F、B、C为顶点的三角形为等腰三角形时,AD的长为$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
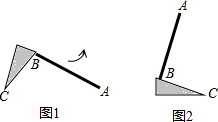 如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为105°.
如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为105°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 52与25 | B. | -ab与ba | C. | 0.2a2b与-$\frac{1}{5}$a2b | D. | a2b3与-a3b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com