
【题目】由甲、乙两个工程队承包某校校园的绿化工程,甲、乙两队单独完成这项工程所需的时间比是5:3,两队共同施工15天可以完成.
(1)求两队单独完成此项工程各需多少天?
(2)此项工程由甲、乙两队共同施工15天完成任务后,学校付给他们20000元报酬,若按各自完成的工程量分配这笔钱,问甲、乙两队各应得到多少元?
【答案】(1)甲队单独完成此项工程需要40天,乙队单独完成此项工程需要24天;(2)甲队应得的报酬为7500元,乙队应得的报酬为12500元.
【解析】
(1)首先表示出两工程队完成需要的时间,进而利用总工作量为1得出等式求出答案;
(2)根据(1)中所求,进而利用两队完成的工作量求出答案.
(1)设甲队单独完成此项工程需要![]() 天,则乙队单独完成此项工程需要
天,则乙队单独完成此项工程需要![]() 天,
天,
根据题意得:![]() ,
,
解得:![]() ,
,
经检验,![]() 是原方程得解,∴
是原方程得解,∴![]() (天),
(天),![]() (天).
(天).
答:甲队单独完成此项工程需要40天,乙队单独完成此项工程需要24天.
(2)甲队应得到![]() (元),
(元),
乙队应得到![]() (元).
(元).
答:甲队应得的报酬为7500元,乙队应得的报酬为12500元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】金堂某养鸭场有1800只鸭准备对外出售.从中随机抽取了一部分鸭,根据它们的质量(单位:![]() ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:

(1)养鸭场随机共抽取鸭______只,并补全条形统计图;
(2)请写出统计的这组数据的众数为______、中位数为_______,并求这组数据的平均数(精确到0.01);
(3)根据样本数据,估计这1800只鸭中,质量为![]() 的约有多少只?
的约有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
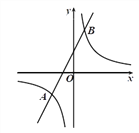
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 与反比例函数
与反比例函数![]() 交于点
交于点![]() ,
, ![]() .
.
(1)分别求出反比例函数和一次函数的表达式;
(2)根据函数图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线![]() 、
、![]() 交于点
交于点![]() ,顺次联结ABCD各边中点得到的一个新的四边形,如果添加下列四个条件中的一个条件:①
,顺次联结ABCD各边中点得到的一个新的四边形,如果添加下列四个条件中的一个条件:①![]() ⊥
⊥![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,可以使这个新的四边形成为矩形,那么这样的条件个数是()
,可以使这个新的四边形成为矩形,那么这样的条件个数是()

A. 1个;B. 2个;
C. 3个;D. 4个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.
(结果精确到1m,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
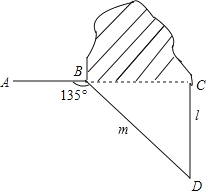
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
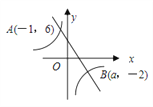
【题目】(8分)如图,一次函数y1=kx+b(k≠0)和反比例函数y2=![]() (m≠0)的图像交于点A(-1,6)、B(a,-2).
(m≠0)的图像交于点A(-1,6)、B(a,-2).
(1)求一次函数与反比例函数的解析式;
(2)根据图像直接写出y1>y2时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是弧![]() 的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
⑴求证:AC=CD.
⑵若OB=2,求BH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为a,b的矩形发生形变后成为边长为a,b的平行四边形,如图1,ABCD中,![]() ,AB边上的高为h,我们把h与a的比值叫做这个平行四边形的“形变比”.
,AB边上的高为h,我们把h与a的比值叫做这个平行四边形的“形变比”.
![]() 画出图2中菱形ABCD形变前的图形.
画出图2中菱形ABCD形变前的图形.
![]() 若图2中菱形ABCD的“形变比”为
若图2中菱形ABCD的“形变比”为![]() ,求菱形ABCD形变前后的面积之比.
,求菱形ABCD形变前后的面积之比.
![]() 当边长为3,4的矩形形变后成为一个内角是
当边长为3,4的矩形形变后成为一个内角是![]() 的平行四边形时,求这个平行四边形的“形变比”.
的平行四边形时,求这个平行四边形的“形变比”.
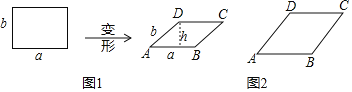
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com