
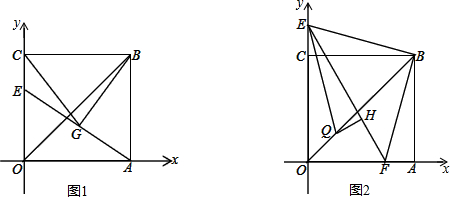
分析 (1)根据方程的解的定义,求出a,可得点B坐标,即可求出△AOB的面积.
(2)结论:∠BGC=2∠OCG.如图1中,作GM⊥BC于M.只要证明GC=GM,即可推出∠MGC=∠MGB,由MG∥OC,推出∠MGC=∠GCO,推出∠CGB=2∠OCG.
(3)结论:②是定值.由△BCE≌△BAF,推出EC=AF,推出OE+OF=OC+CE+OA-AF=2OA=6,由OB平分∠FOE,QE平分∠OEF,推出点Q是△EOF的内心,由QH⊥EF,QN⊥EO,QP⊥OF,推出QH=QN=QP=$\frac{OE+OF-EF}{2}$,由此即可解决问题.
解答 解:(1)∵a是关于x的方程$\frac{x-1}{2}$+a=4的解,
∴$\frac{a-1}{2}$+a=4,
∴a=3,
∴B(3,3),
∵BA⊥x轴,
∴S△ABO=$\frac{1}{2}$×3×3=$\frac{9}{2}$.
(2)结论:∠BGC=2∠OCG.
理由:如图1中,作GM⊥BC于M.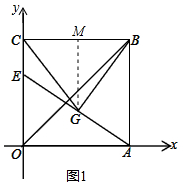
∵四边形ABCO是正方形,
∴AB∥OC,BC∥OA,
∵EG=GA,GM∥CE∥AB,
∴CM=MB,
∴GC=GB,
∴∠MGC=∠MGB,
∵MG∥OC,
∴∠MGC=∠GCO,
∴∠CGB=2∠OCG.
(3)结论:②是定值.
理由:如图2中,作QP⊥OA于P,QN⊥OC于N.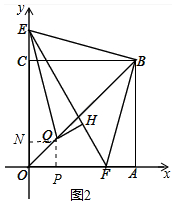
∵∠EBF=∠CBA=90°,
∴∠EBC=∠ABF,
在△BCE和△BAF中,
$\left\{\begin{array}{l}{∠BCE=∠BAF}\\{∠EBC=∠ABF}\\{BC=AB}\end{array}\right.$,
∴△BCE≌△BAF,
∴EC=AF,
∴OE+OF=OC+CE+OA-AF=2OA=6,
∵OB平分∠FOE,QE平分∠OEF,
∴点Q是△EOF的内心,
∵QH⊥EF,QN⊥EO,QP⊥OF,
∴QH=QN=QP=$\frac{OE+OF-EF}{2}$,
∴QH=$\frac{EO+OF}{2}$-$\frac{1}{2}$EF,
∴$\frac{1}{2}$EF+QH=$\frac{EO+OF}{2}$=3=定值.
点评 本题考查三角形综合题、正方形的判定和性质、全等三角形的判定和性质、直角三角形的内切圆半径等知识,解题的关键是记住直角三角形内切圆半径r=$\frac{a+b-c}{2}$,学会添加常用辅助线,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
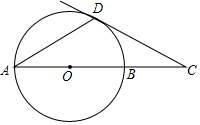 如图1,⊙O的直径AB=2,⊙O的切线CD与AB的延长线交于点C,D为切点,∠C=30°,则AD等于( )
如图1,⊙O的直径AB=2,⊙O的切线CD与AB的延长线交于点C,D为切点,∠C=30°,则AD等于( )| A. | $\sqrt{3}$ | B. | 2 | C. | 1 | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
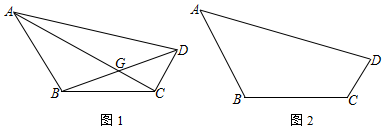
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知⊙O的内接四边形ABCD,AD=$\sqrt{2}$,CD=1,半径为1,则∠B的度数为( )
如图,已知⊙O的内接四边形ABCD,AD=$\sqrt{2}$,CD=1,半径为1,则∠B的度数为( )| A. | 60° | B. | 70° | C. | 75° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
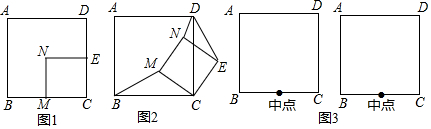
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com