
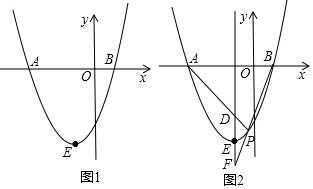
分析 (1)通过解方程a(x+3)(x-1)=0可得到A、B的坐标,从而得到抛物线的对称轴为直线x=-1,则顶点坐标为(-1,-4),然后把顶点坐标代入解析式可求出a的值;
(2)利用抛物线解析式得到抛物线与y轴的交点坐标为(0,-3),利用∠PAB=45°可判定点P为抛物线与y轴的交点,于是得到点P的坐标为(-3,0);
(3)作PH⊥x轴于H,如图,设P(t,t2+2t-3),证明△ACD∽△AHP,利用相似比得到CD=-2(t-1)=2-2t,再证明△BHP∽△BCF,利用相似比得到CF=2(t+3)=6+2t,上,CD+CF=8.
解答 解:(1)当y=0时,a(x+3)(x-1)=0,解得x1=-3,x2=1,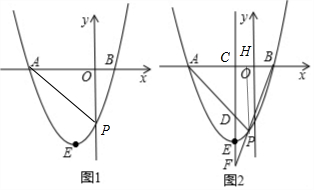
则A(-3,0),B(1,0),
∴抛物线的对称轴为直线x=-1,
当x=-1时,a•2•(-2)=-4,解得a=1;
(2)抛物线解析式为y=(x+3)(x-1)=x2+2x-3,
当x=0时,y=x2+2x-3=-3,则抛物线与y轴的交点坐标为(0,-3),
∵∠PAB=45°,
∴点P为抛物线与y轴的交点.
∴点P的坐标为(-3,0);
(3)CD+CF为定值.
作PH⊥x轴于H,如图,
设P(t,t2+2t-3),
∵CD∥PH,
∴△ACD∽△AHP,
∴$\frac{AC}{AH}$=$\frac{CD}{PH}$,即$\frac{2}{t+3}$=$\frac{CD}{-({t}^{2}+2t-3)}$,
∴CD=-2(t-1)=2-2t,
∵PH∥CF,
∴△BHP∽△BCF,
∴$\frac{PH}{CF}$=$\frac{BH}{BC}$,即$\frac{-({t}^{2}+2t-3)}{CF}$=$\frac{1-t}{2}$,
∴CF=2(t+3)=6+2t,
∴CD+CF=2-2t+6+2t=8.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质;会利用待定系数法求二次函数解析式,会求抛物线与坐标轴的交点坐标;会利用相似比表示线段之间的关系.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小刘从家里骑自行车出发,去镇上超市途中碰到妹妹甜甜走路从镇上回家,小刘在超市买完东西回家,在回去的路上又碰到了甜甜,便载甜甜一起回家,结果小刘比正常速度回家的时间晚了3分钟,二人离镇的距离S(千米)和小刘从家出发后的时间t(分钟)之间的关系如图所示,(假设二人之间交流时间忽略不计)
小刘从家里骑自行车出发,去镇上超市途中碰到妹妹甜甜走路从镇上回家,小刘在超市买完东西回家,在回去的路上又碰到了甜甜,便载甜甜一起回家,结果小刘比正常速度回家的时间晚了3分钟,二人离镇的距离S(千米)和小刘从家出发后的时间t(分钟)之间的关系如图所示,(假设二人之间交流时间忽略不计)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
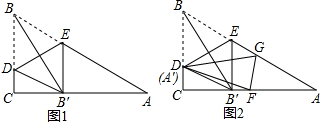
 已知△ABC的三边长分别为AB=2$\sqrt{5}$,AC=2,BC=4$\sqrt{\frac{1}{2}}$.
已知△ABC的三边长分别为AB=2$\sqrt{5}$,AC=2,BC=4$\sqrt{\frac{1}{2}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com