
【题目】如图,(1)∠2与∠B是什么角?若∠1=∠B,则∠2与∠B有何数量关系?请说明理由.
(2)∠3与∠C是什么角?若∠4+∠C=180°,则∠3与∠C有何数量关系?请说明理由.
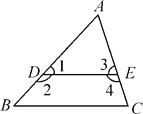
【答案】(1)同旁内角,∠2+∠B=180°.理由见解析. (2)同位角,∠3=∠C.理由见解析.
【解析】
方法一:根据“同角或等角的补角相等”即可解答;
方法二:根据“同位角相等,两直线平行”推知DE∥BC,则由“两直线平行,同旁内角互补”得到∠2+∠B=180°;由“同旁内角互补,两直线平行”和“两直线平行,同位角相等”得到∠3=∠C.
解:方法一:(1)同旁内角,∠2+∠B=180°.理由:因为∠1+∠2=180°,∠1=∠B,所以∠2+∠B=180°;(2同位角,∠3=∠C.理由:∠4+∠C=180°,∠4+∠3=180°,所以∠3=∠C.
方法二:解:∠2+∠B=180°.理由如下:
∵∠1=∠B,
∴DE∥BC,
∴∠2+∠B=180°.
∵∠4+∠C=180,
∴DE∥BC,
∴∠3=∠C.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() )
)
例2 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() 或
或![]() 或
或![]() )
)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.
的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,![]() 的度数不同,得到
的度数不同,得到![]() 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形![]() 中,设
中,设![]() ,当
,当![]() 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读思考
我们知道,在数轴上|a|表示数a所对应的点到原点的距离,这是绝对值的几何意义,由此我们可进一步地来研究数轴上任意两个点之间的距离,一般地,如果数轴上两点A、B 对立的数用a,b表示,那么这两个点之间的距离AB=|a﹣b|.也可以用两点中右边的点所表示数的减去左边的点所表示的数来计算,例如:数轴上P,Q两点表示的数分别是﹣1和2,那么P,Q两点之间的距离就是 PQ=2﹣(﹣1)=3.
启发应用
如图,点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0
(1)求线段AB的长;
(2)如图,点C在数轴上对应的数为x,且x是方程2x+1=![]() x﹣8的解,
x﹣8的解,
①求线段BC的长;
②在数轴上是否存在点P使PA+PB=BC?若存在,直接写出点P对应的数:若不存在,说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表:
组别 | 观点 | 频数(人数) |
A | 大气气压低,空气不流动 | 80 |
B | 地面灰尘大,空气湿度低 | m |
C | 汽车尾气排放 | n |
D | 工厂造成的污染 | 120 |
E | 其他 | 60 |
请根据图表中提供的信息解答下列问题: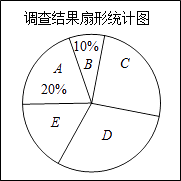
(1)填空:m= , n= .
(2)若该市人口约有100万人,请你计算其中持D组“观点”的市民人数是多少万人?
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,(1)指出DC和AB被AC所截得的内错角;
(2)指出AD和BC被AE所截得的同位角;
(3)指出∠4与∠7,∠2与∠6,∠ADC与∠DAB各是什么关系的角,并指出各是哪两条直线被哪一条直线所截形成的.
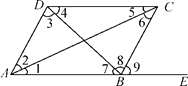
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在线段AB上,点M、N分别是AC、BC的中点.
(1)若AC = 8,CB = 6,求线段MN的长;
(2)若AC = a,MN = b,求线段BC的长用含![]() ,
,![]() 的代数式可以表示.
的代数式可以表示.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写推理理由,将过程补充完整:
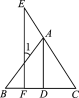
如图,已知AD⊥BC于点D,EF⊥BC于点F,AD平分∠BAC.求证:∠E=∠1.
证明:∵AD⊥BC,EF⊥BC(已知),
∴∠ADC=∠EFC=90°(垂直的定义).
∴____________(_____________).
∴∠1=_____(_____________),
∠E=_____(_______________).
又∵AD平分∠BAC(已知),
∴_____=________.
∴∠1=∠E(等量代换).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=x2+bx+c与y=x的图象如图所示,有以下结论: ①b2﹣4c>0;
②b+c+1=0;
③3b+c+6=0;
④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E,F在边BC上,点P在线段AD上,若PE∥AB,∠PFD=∠C,点D到AB和AC的距离相等.求证:点D到PE和PF的距离相等.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com