
【题目】如图为两正方形ABCD、BEFG和矩形DGHI的位置图,其中G、F两点分别在BC、EH上.若AB=5,BG=3,则△GFH的面积为何?( ) 
A.10
B.11
C.![]()
D.![]()
【答案】D
【解析】解:∵四边形ABCD,BEFG是正方形, ∴BC=CD=AB=5,GF=BG=3,∠C=∠BGF=∠GFE=∠CGF=∠GFH=90°,
∵四边形DGHI是矩形,
∴∠DGH=90°,
∴∠DGC+∠CGH=∠FGH+∠HGC=90°,
∴∠DGC=∠FGH,
∴△DGC∽△HGF,
∴ ![]() =
= ![]() ,
,
∴FH= ![]() =
= ![]() =
= ![]() ,
,
∴S△FHG= ![]() GFFH=
GFFH= ![]() ,
,
故选D.
【考点精析】利用矩形的性质和正方形的性质对题目进行判断即可得到答案,需要熟知矩形的四个角都是直角,矩形的对角线相等;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD,CE分别为AC,AB边上的中线,BD⊥CE,若BD=4,CE=6,则△ABC的面积为( )
A.12
B.24
C.16
D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张前往某精密仪器产应聘,公司承诺工资待遇如图.进厂后小张发现:加工1件A型零件和3件B型零件需5小时;加工2件A型零件和5件B型零件需9小时. 工资待遇:每月工资至少3000元,每天工作8小时,每月工作25天,加工1件A型零件计酬16元,加工1件B型零件计酬12元,月工资=底薪(800元)+计件工资.
(1)小张加工1件A型零件和1件B型零件各需要多少小时?
(2)若公司规定:小张每月必须加工A、B两种型号的零件,且加工B型的数量不大于A型零件数量的2倍,设小张每月加工A型零件a件,工资总额为W元,请你运用所学知识判断该公司颁布执行此规定后是否违背了工资待遇承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为4,E是BC边上的一个动点,AE⊥EF,EF交DC于点F,设BE=x,FC=y,则当点E从点B运动到点C时,y关于x的函数图象是( )
A.
B.
C.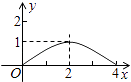
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=kx+b的图象与反比例函数y2= ![]() 的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=
的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2= ![]() 的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B 
(1)求m的值;
(2)求一次函数的表达式;
(3)根据图象,当y1<y2<0时,写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,面积为6的平行四边形纸片ABCD中,AB=3,∠BAD=45°,按下列步骤裁剪和拼图. 
第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
则由纸片拼成的五边形PMQRN中,BD= , 对角线MN长度的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB是⊙O的直径,E是AB延长线上一点,EC切⊙O于点C,OP⊥AO交AC于点P,交EC的延长线于点D.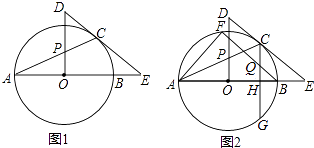
(1)求证:△PCD是等腰三角形;
(2)CG⊥AB于H点,交⊙O于G点,过B点作BF∥EC,交⊙O于点F,交CG于Q点,连接AF,如图2,若sinE= ![]() ,CQ=5,求AF的值.
,CQ=5,求AF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com