
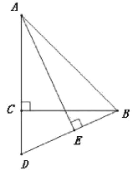
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D为AC延长线上一点,连接BD,AE⊥BD于点E.
(1)记△ABC得外接圆为⊙0,
①请用文字描述圆心0的位置;
②求证:点E一定在⊙0上.
(2)将射线AE绕点A顺时针旋转45°后,所得到的射线与BD延长线交于点F,连接CF,CE.
①依题意补全图形;
②用等式表示线段AF,CE,BE的数量关系,并证明.
【答案】(1)证明见解析(2)AF=2CE+![]() BE
BE
【解析】
(1)连接OC,OE, 可得OC=OE=OA=OB=![]() AB,即点E在以O为圆心,OA为半径的圆上,
AB,即点E在以O为圆心,OA为半径的圆上,
即点E在△ABC的外接圆⊙O上.
(2) 过点C作CG⊥CE,与BF交于点G,可证的∠BCG=∠ECA及△ACE≌△BCG(ASA),可得BG=AE,EC=GC,由旋转的性质可得∠EFA=90°-∠EAF=45°=∠EAF,AE=EF,可得AF=2CE+![]() BE.
BE.
(1)①线段AB的中点;
②证明:如图, 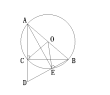
连接OC,OE,
∵AE⊥BD,
∴∠AEB=90°,
∵∠ACB=90°,O为AB中点,
∴OC=OE=OA=OB=![]() AB,
AB,
∴点E在以O为圆心,OA为半径的圆上,
即点E在△ABC的外接圆⊙O上.
(2)①如上图中所示, 
②AF=2CE+![]() BE;
BE;
证明如下:
过点C作CG⊥CE,与BF交于点G.
∴∠ECG=∠BCA=90°,
∴∠ECG+∠BCE=∠BCA+∠BCE,
即∠BCG=∠ECA.
∵E,A,B,C在以O为圆心,OA为半径的圆上,
∴∠EAC=∠EBC.
∵BC=AC,
∴△ACE≌△BCG(ASA)
∴BG=AE,EC=GC.
∴在Rt△CEG中,EG=![]() .
.
∵由旋转,∠EAF=45°,而∠AEF=90°,
∴∠EFA=90°-∠EAF=45°=∠EAF,
∴AE=EF,
∴在Rt△AEF中,AF=![]() .
.
∵BG=BE+EG=BE+![]() CE,
CE,
∴AF=2CE+![]() BE.
BE.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图①,一台灯放置在水平桌面上,底座AB与桌面垂直,底座高AB=5cm,连杆BC=CD=20cm,BC,CD与AB始终在同一平面内.

(1)如图②,转动连杆BC,CD,使∠BCD成平角,∠ABC=143°,求连杆端点D离桌面l的高度DE.
(2)将图②中的连杆CD再绕点C逆时针旋转16°,如图③,此时连杆端点D离桌面l的高度减小了 cm.
(参考数据:sin37°=0.6,cos37°=0.8,tan37°=0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物线y=![]() x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=
x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=![]() x2+bx+c交于第四象限的F点.
x2+bx+c交于第四象限的F点.

(1)求该抛物线解析式与F点坐标;
(2)如图,动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;
同时,动点M从点A出发,沿线段AE以每秒![]() 个单位长度的速度向终点E运动.过
个单位长度的速度向终点E运动.过
点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.
①问EP+PH+HF是否有最小值,如果有,求出t的值;如果没有,请说明理由.
②若△PMH是等腰三角形,求出此时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机摸取一个小球然后放回,再随机摸出一个小球.
(Ⅰ)请用列表法(或画树状图法)列出所有可能的结果;
(Ⅱ)求两次取出的小球标号相同的概率;
(Ⅲ)求两次取出的小球标号的和大于6的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
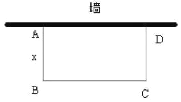
【题目】如图,园林小组的同学用一段长16米的篱笆围成一个一边靠墙的矩形菜园ABCD,墙的长度为9米,设AB的长为x米,BC的长为y米.
(1)①写出y与x的函数关系是: ;
②自变量x的取值范围是 ;
(2)园林小组的同学计划使矩形菜园的面积为30平方米,试求此时边AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
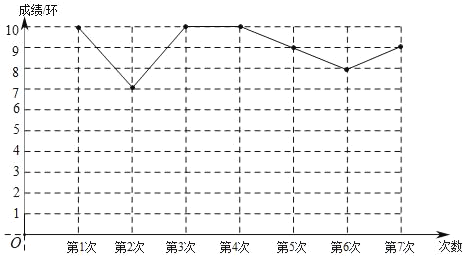
【题目】嘉淇同学利用业余时间进行射击训练,一共射击7次,经过统计,制成如图12所示的折线统计图.
(1)这组成绩的众数是 ;
(2)求这组成绩的方差;
(3)若嘉淇再射击一次(成绩为整数环),得到这8次射击成绩的中位数恰好就是原来7次成绩的中位数,求第8次的射击成绩的最大环数.
查看答案和解析>>
科目:初中数学 来源: 题型:
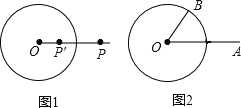
【题目】如图1,⊙O的半径为r,若点P′在射线OP上,满足OP′×OP=r2,则称点P′是点P关于⊙O的“反演点”,如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A'是点A关于⊙O的反演点,求A'B的长为( )
A.![]() B.2
B.2![]() C.2D.4
C.2D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
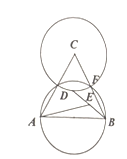
【题目】如图,已知等边△ABC的边长为4,以AB为直径的圆交BC于点F,CF为半径作圆,D是⊙C上一动点,E是BD的中点,当AE最大时,BD的长为( )
A.![]() B.
B.![]() C.4D.6
C.4D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有四个球,这四个球上分别标记数字﹣3、﹣1、0、2,除数字不同外,这四个球没有任何区别.
(1)从中任取一球,求该球上标记的数字为正数的概率;
(2)从中任取两球,将两球上标记的数字分别记为x、y,求点(x,y)位于第二象限的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com