
 ��������������y=$\frac{k}{x}$��y=$\frac{1}{x}$�ڵ�һ�����ڣ���P��y=$\frac{k}{x}$��ͼ���ϣ�PC��ֱ��X���ڵ�C����y=$\frac{1}{x}$��ͼ���ڵ�A��PD��ֱ��Y����D����y=$\frac{1}{x}$��ͼ���ڵ�B������P��y=$\frac{k}{x}$��ͼ�����˶�ʱ�����н��۴�����ǣ�������
��������������y=$\frac{k}{x}$��y=$\frac{1}{x}$�ڵ�һ�����ڣ���P��y=$\frac{k}{x}$��ͼ���ϣ�PC��ֱ��X���ڵ�C����y=$\frac{1}{x}$��ͼ���ڵ�A��PD��ֱ��Y����D����y=$\frac{1}{x}$��ͼ���ڵ�B������P��y=$\frac{k}{x}$��ͼ�����˶�ʱ�����н��۴�����ǣ�������| A�� | ��ODB���OCA�������� | |
| B�� | ����A��PC���е�ʱ����Bһ����PD���е� | |
| C�� | ֻ�е��ı���OCPBΪ������ʱ���ı���PAOB�������� | |
| D�� | $\frac{CA}{PA}$=$\frac{DB}{PB}$ |
���� ���ݷ�����������ͼ������ʣ��ر��Ǹ��ݷ���������k�ļ������壬���ĸ�ѡ����һ���з��������ɵó���ȷ�𰸣�
��� �⣺A�����ڵ�A�͵�D����ͬһ������������y=$\frac{1}{2}$��ͼ���ϣ�����S��ODB=$\frac{1}{2}$��S��OCA=$\frac{1}{2}$���ʡ�ODB���OCA�������ȣ���A��ȷ��
B������OP����A��PC���е㣬
���OAP�͡�OAC�������ȣ�
�ߡ�ODP�����=��OCP�����=$\frac{k}{2}$����ODB���OCA�������ȣ�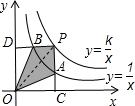
���OBP���OAP�������ȣ�
���OBD�͡�OBP�����ȣ�
���Bһ����PD���е㣬��B��ȷ��
C�����ھ���OCPD��������ODB��������OCAΪ��ֵ�����ı���PAOB��������ᷢ���仯����C����
D����P��m��$\frac{k}{m}$������A��m��$\frac{1}{m}$����B��$\frac{m}{k}$��$\frac{k}{m}$������CA=$\frac{1}{m}$��PA=$\frac{k}{m}$-$\frac{1}{m}$��DB=$\frac{m}{k}$��PB=m-$\frac{m}{k}$��
��$\frac{CA}{PA}=\frac{\frac{1}{m}}{\frac{k}{m}-\frac{1}{m}}=\frac{1}{k-1}$��$\frac{DB}{PB}=\frac{1}{k-1}$��
��$\frac{CA}{PA}=\frac{DB}{PB}$����D��ȷ��
��ѡC��
���� ���⿼���˷������������ۺ��⣬�ؼ�����P�����꣬���õ����������ϵ�����������������ʱ�ʾ����߶εij�����ÿһ�����۽����жϣ�


 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | 10��1�� | 10��2�� | 10��3�� | 10��4�� | 10��5�� | 10��6�� | 10��7�� |
| �����仯 �����ˣ� | +2.1 | +1.78 | +0.2 | -0.8 | -1 | -1.6 | -1.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���x�ᡢy����������Ϸֱ��ȡOA��OB��ʹOA=OB���ٷֱ��Ե�A��BΪԲ�ģ��Դ���$\frac{1}{2}$AB��Ϊ�뾶�������������ڵ�C������C������Ϊ��m-1��2n������m��n�Ĺ�ϵΪm-1=2n��
��ͼ����ƽ��ֱ������ϵ�У���x�ᡢy����������Ϸֱ��ȡOA��OB��ʹOA=OB���ٷֱ��Ե�A��BΪԲ�ģ��Դ���$\frac{1}{2}$AB��Ϊ�뾶�������������ڵ�C������C������Ϊ��m-1��2n������m��n�Ĺ�ϵΪm-1=2n���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com