
【题目】如图所示,以△ABC的两边AB、AC为边向外作等边△ABD和等边△ACE,DC、BE相交于点O.
(1)求证:DC=BE;
(2)求∠BOC的度数;
(3)当∠BAC的度数发生变化时,∠BOC的度数是否变化?若不变化,请求出∠BOC的度数;若发生变化,请说明理由.

【答案】(1)证明见解析; (2)∠BOC=120°;(3)当∠BAC的度数发生变化时,∠BOC的度数不变.∠BOC=120°.
【解析】
(1)易证∠DAB=∠EAC=60°,AD=AB,AE=AC,即可求得∠DAC=∠BAE,即可证明△DAC≌△BAE;
(2)根据(1)中结论可得∠ADC=∠ABE,即可求得∠ODB+∠OBD=∠ADB+∠ABD,根据三角形外角性质即可解题;
(3)由(2)可得∠ODB+∠OBD=∠ADB+∠ABD,因此可以判定∠BOC和∠BAC大小无关.
(1)证明:∵△ADB和△AEC都是等边三角形,
∴∠DAB=∠EAC=60°,AD=AB,AE=AC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
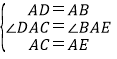 ,
,
∴△DAC≌△BAE(SAS);
∴DC=BE
(2)解:∵△DAC≌△BAE,
∴∠ADC=∠ABE,
∴∠ODB+∠OBD=∠ADB-∠ADC+∠ABD+∠ABE=∠ADB+∠ABD=120°,
∴∠BOC=∠ODB+∠OBD=120°,
(3)解:∵由(2)可得∠ODB+∠OBD=∠ADB+∠ABD,
∴∠BOC和∠BAC大小无关.


科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆小汽车在高速公路上从静止到起动10秒内的速度经测量如下表:

(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用T表示时间,V表示速度,那么随着T的变化,V的变化趋势是什么?
(3)当T每增加1秒,V的变化情况相同吗?在哪1秒钟,V的增加最大?
(4)若高速公路上小汽车行驶速度的上限为120千米/小时,试估计大约还需几秒这辆小汽车的速度就将达到这个上限.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第一象限内,点P(2,3),M(a,2)是双曲线y= ![]() (k≠0)上的两点,PA⊥x轴于点A,MB⊥x轴于点B,PA与OM交于点C,则△OAC的面积为 .
(k≠0)上的两点,PA⊥x轴于点A,MB⊥x轴于点B,PA与OM交于点C,则△OAC的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上A 点对应的数为﹣5,B 点在A 点右边,电子蚂蚁甲、乙在B分别以2个单位/秒、1个单位/秒的速度向左运动,电子蚂蚁丙在A 以3个单位/秒的速度向右运动.
(1)若电子蚂蚁丙经过5秒运动到C 点,求C 点表示的数;
![]()
(2)若它们同时出发,若丙在遇到甲后1秒遇到乙,求B 点表示的数;
![]()
(3)在(2)的条件下,设它们同时出发的时间为t 秒,是否存在t的值,使丙到乙的距离是丙到甲的距离的2倍?若存在,求出t 值;若不存在,说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示.在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的中垂线,E、N在BC上,则∠EAN=( )

A. 58° B. 32° C. 36° D. 34°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小红想用一条彩带缠绕易拉罐,正好从A点绕到正上方B点共四圈,已知易拉罐底面周长是12 cm,高是20 cm,那么所需彩带最短的是( )

A. 13 cm B. 4![]() cm C. 4
cm C. 4![]() cm D. 52 cm
cm D. 52 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,小刚一家乘车去离家380公里的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示. 
(1)从小刚家到该景区乘车一共用了多少时间?
(2)求线段AB对应的函数解析式;
(3)小刚一家出发2.5小时时离目的地多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①②,![]() 的两边分别平行.
的两边分别平行.
(1)在图①中,![]() 与
与![]() 有什么数量关系?为什么?
有什么数量关系?为什么?
(2)在图②中,![]() 与
与![]() 有什么数量关系?为什么?
有什么数量关系?为什么?
(3)由(1)(2)你能得出什么结论?用一句话概括你得到的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com