练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    规定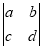＝ad－bc，若＝6，则－11x2＋6＝________．

    7 【解析】∵＝ad－bc， ∴＝-5（x2-3）-2（3x2+5）=-5x2+15-6x2-10=-11x2+5， ∵＝6，∴-11x2+5=6，∴-11x2=1，∴-11x2+6=1+6=7， 故答案为：7.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年甘肃省武威市凉州区洪祥镇九年级（上）期末数学试卷 题型：填空题

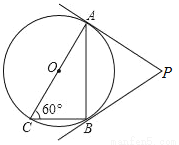
    如图，AC是⊙O的直径，∠ACB=60°，连接AB，过A、B两点分别作⊙O的切线，两切线交于点P．若已知⊙O的半径为1，则△PAB的周长为_____．

    【解析】根据圆周角定理的推论及切线长定理，即可得出答案 【解析】 ∵AC是⊙O的直径， ∴∠ABC=90°， ∵∠ACB=60°， ∴∠BAC=30°， ∴CB=1，AB=， ∵AP为切线， ∴∠CAP=90°， ∴∠PAB=60°， 又∵AP=BP， ∴△PAB为正三角形， ∴△PAB的周长为3．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级下册 期中测试卷 题型：解答题

    如图，Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点B出发，在BA边上以每秒5cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接PQ．

    （1）若△BPQ与△ABC相似，求t的值；

    （2）连接AQ、CP，若AQ⊥CP，求t的值．

    (1) t=1或 ;(2) 【解析】试题分析： （1）由∠B是△BPQ与△ABC的公共角，可知，若两三角形相似，存在两种情况：①△BPQ∽△BAC；②△BPQ∽△BCA；分这两种情况结合相似三角形的性质和题意即可解得对应的t的值； （2）如图1，过P作PM⊥BC于点M，AQ，CP交于点N，由题意可知：当AQ⊥CP时，△ACQ∽△CMP，由相似三角形的性质列出比例式即可解得对应的t...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级下册 期中测试卷 题型：单选题

    如图，在△ABC中，点D、E分别在边AB、AC上，下列条件中不能判断△ABC∽△AED的是（ ）

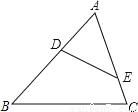
    A．∠AED=∠B B．∠ADE=∠C C． D．

    D. 【解析】 试题解析：∵∠DAE=∠CAB， ∴当∠AED=∠B或∠ADE=∠C时，△ABC∽△AED； 当时，△ABC∽△AED． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第3章 整式及其加减 单元测试卷 题型：解答题

    若代数式(4x2－mx－3y＋4)－(8nx2－x＋2y－3)的值与字母x的取值无关，求代数式(－m2＋2mn－n2)－2(mn－3m2)＋3(2n2－mn)的值．

    . 【解析】试题分析：已知代数式去括号合并后，根据结果与x的取值无关，求出m与n的值，原式去括号合并后代入数值进行计算即可求出代数式的值. 试题解析：(4x2－mx－3y＋4)－(8nx2－x＋2y－3) ＝4x2－mx－3y＋4－8nx2＋x－2y＋3 ＝(4－8n)x2＋(1－m)x－5y＋7， ∵上式的值与字母x的取值无关， ∴4－8n＝0，1－m＝0，即...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第3章 整式及其加减 单元测试卷 题型：填空题

    钢笔每支a元，铅笔每支b元，买2支钢笔和3支铅笔共需________元．

    (2a＋3b) 【解析】∵钢笔每支a元，铅笔每支b元， ∴买2支钢笔、3支铅笔共付钱（2a+3b）元， 故答案为：（2a+3b）．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第3章 整式及其加减 单元测试卷 题型：单选题

    若m﹣n=﹣1，则（m﹣n）2﹣2m+2n的值是（　　）

    A. 3 B. 2 C. 1 D. ﹣1

    A 【解析】试题分析：因为m－n = －1，所以（m－n）2－2m+2n=（m－n）2－2（m-n）=1+2=3，故选：A.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学人教版上册：第4章 几何图形初步 单元测试卷 题型：填空题

    如图，为抄近路践踏草坪是一种不文明的现象，请你用数学知识解释出这一现象的原因 ．

    两点之间线段最短 【解析】试题分析：根据线段的性质解答即可． 【解析】 为抄近路践踏草坪原因是：两点之间线段最短． 故答案为：两点之间线段最短．

    查看答案和解析>>

    科目：初中数学 来源：云南省楚雄州2017-2018学年上学期期末教学质量监测九年级数学试卷 题型：解答题

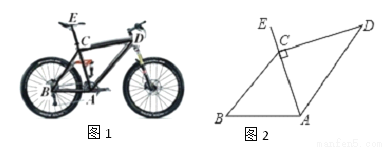
    为倡导“低碳生活”，人们现在常选择以自行车作为代步工具，如图1所示是一辆自行车的实物图，车架档AC与CD的长分别为45cm，60cm，且它们互相垂直，座杆CE的长为20cm，点A，C，E在同一条直线上，且∠CAB=75°，如图2．

    （1）求车架档AD的长；

    （2）求车座点E到车架档AB的距离．

    （结果精确到1cm．参考数据：sin75°≈0.966，cos75°≈0.259，tan75°≈3.732）．

    （1）75cm；（2）63cm. 【解析】试题分析：（1）在RT△ACD中利用勾股定理求AD即可． （2）过点E作EF⊥AB，在RT△EFA中，利用三角函数求EF=AEsin75°，即可得到答案． 试题解析：（1）∵在RT△ACD中，AC=45cm，DC=60cm，∴AD==75，∴车架档AD的长为75cm， （2）过点E作EF⊥AB，垂足为点F，∵AE=AC+CE=45+...

    查看答案和解析>>

    同步练习册答案