
分析 (1)只要证明A、D、C、E四点共圆,即可得到∠ECM=∠DAE=60°,∠AED=∠ACB=60°,所以∠DAE=∠DEA由此解决问题.
(2)证明类似(1),先证明A、D、C、E四点共圆,再证明∠DAE=∠DEA即可.
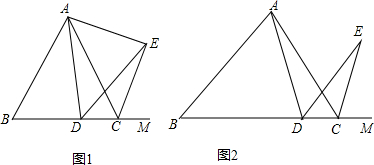
解答 (1)证明: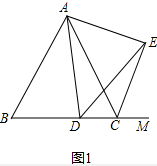 如图1中,∵△ABC是等边三角形,
如图1中,∵△ABC是等边三角形,
∴∠ACB=60°,∠ACM=120°,
∴CE平分∠ACM,
∴∠ACE=∠ECM=60°,
∵∠ADE=60°,∠ACE=60°,
∴∠ADE=∠ACE,
∴A、D、C、E四点共圆,
∴∠ECM=∠DAE=60°,∠AED=∠ACB=60°,
∴∠DAE=∠DEA,
∴AD=DE.
(2)结论成立.DA=DE.
理由:如图2中,连接AE,
∵∠ACB=60°,
∴∠ACM=180°-∠ACB=120°,
∴CE平分∠ACM,
∴∠ACE=∠ECM=60°,
∵∠ADE=60°,∠ACE=60°,
∴∠ADE=∠ACE,
∴A、D、C、E四点共圆,
∴∠ECM=∠DAE=60°,∠AED=∠ACB=60°,
∴∠DAE=∠DEA,
∴AD=DE.
点评 本题考查四点共圆,圆内接四边形的性质等知识,解题的关键是发现A、D、C、E四点共圆,掌握圆内接四边形的性质,题目有点难度.


科目:初中数学 来源: 题型:解答题
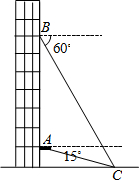 从一幢建筑大楼的两个观察点A,B观察地面的花坛(点C),测得俯角分别为15°和60°,如图,直线AB与地面垂直,AB=50米,试求出点B到点C的距离.(结果保留根号)
从一幢建筑大楼的两个观察点A,B观察地面的花坛(点C),测得俯角分别为15°和60°,如图,直线AB与地面垂直,AB=50米,试求出点B到点C的距离.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
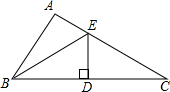 如图,已知△ABC中,AB<AC,BC边上的垂直平分平分线DE交BC于点D,交AC于点E,若AC=10cm,△ABE的周长为18cm,求AB的长.
如图,已知△ABC中,AB<AC,BC边上的垂直平分平分线DE交BC于点D,交AC于点E,若AC=10cm,△ABE的周长为18cm,求AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
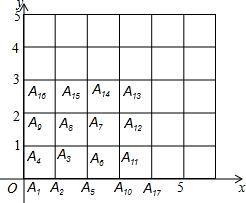 如图所示,已知点A1的坐标为(0,0),点A2的坐标为(1,0),点A3的坐标为(1,1),点A4的坐标为(0,1),A5的坐标为(2,0),点A6坐标为(2,1),点A7的坐标为(2,2),点A8的坐标为(1,2),点A9的坐标为(0,2),点A10的坐标为(3,0),点A11的坐标为(3,1),…,依此规律排列下去,则点A25的坐标为(0,4),点A2015的坐标为(34,44).
如图所示,已知点A1的坐标为(0,0),点A2的坐标为(1,0),点A3的坐标为(1,1),点A4的坐标为(0,1),A5的坐标为(2,0),点A6坐标为(2,1),点A7的坐标为(2,2),点A8的坐标为(1,2),点A9的坐标为(0,2),点A10的坐标为(3,0),点A11的坐标为(3,1),…,依此规律排列下去,则点A25的坐标为(0,4),点A2015的坐标为(34,44).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
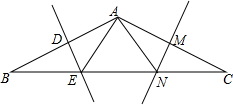 在△ABC中,AB=AC,BC=12,∠B=30°,AB的垂直平分线DE交BC边于点E,AC的垂直平分线MN交BC于点N.
在△ABC中,AB=AC,BC=12,∠B=30°,AB的垂直平分线DE交BC边于点E,AC的垂直平分线MN交BC于点N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com