
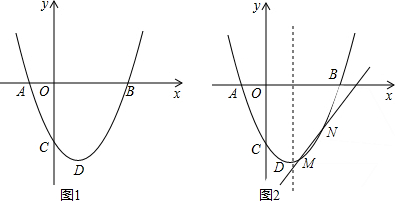
���� ��1���ɡ�ABD�ǵ���ֱ��������ȷ����D��1��-2�����ô���ϵ����ȷ����������ϵʽ��
��2���ɡ�ABCΪ���������Σ����ù��ɶ������a���ɣ�
��3��������������ֱ��y=$\frac{5}{4}$x-4����M��N���㣬�����M��N�����꣬���öԳ��������G��H�����꼴�ɣ�
��� �⣺��1����ͼ1��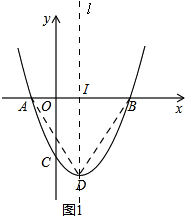
�ߡ�ABD�ǵ���ֱ�������Σ�
�����D��ֱ��l��y�ᣬֱ��l��x�ύ�ڵ�I��
��AI=ID=IB=$\frac{1}{2}$AB=2��
��D��1��-2����
����y=a��x+1����x-3��=ax2-2ax-3a��
��a-2a-3a=-2��
��a=$\frac{1}{2}$��
��y=$\frac{1}{2}$x2-x-$\frac{3}{2}$��
��2���ߡ�ABCΪ���������Σ�
���AB=BC=4��
��OC=$\sqrt{C{B}^{2}-O{B}^{2}}$=$\sqrt{7}$��
��-3a=-$\sqrt{7}$��
��a=$\frac{\sqrt{7}}{3}$��
��AB=AC=4��
��OC=$\sqrt{A{C}^{2}-O{A}^{2}}$=$\sqrt{15}$��
��C��0��-$\sqrt{15}$����
��-3a=-$\sqrt{15}$��
��a=$\frac{\sqrt{15}}{3}$��
��3����ͼ2��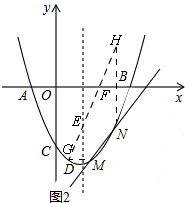
����������ֱ��y=$\frac{5}{4}$x-4����M��N���㣬
��$\left\{\begin{array}{l}{y=\frac{1}{2}��x+1����x-3��}\\{y=\frac{5}{4}x-4}\end{array}\right.$��
��$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=-\frac{3}{2}}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=\frac{5}{2}}\\{{y}_{2}=-\frac{7}{8}}\end{array}\right.$��
��M��2��-$\frac{3}{2}$����N��$\frac{5}{2}$��-$\frac{7}{8}$����
����M���ڶԳ���l�ĶԳƵ�G��
��N����x��ĶԳƵ�H��
����GH��l��E��x����F��
��EM=EG��FN=FH
���P�˶�����·��ΪGH��
��G��0��-$\frac{3}{2}$����H��$\frac{5}{2}$��$\frac{7}{8}$����
��GH=$\frac{\sqrt{761}}{8}$��
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ���������ʽ�����������ε����ʣ��ԳƵ��ص㣮��ͼ��Ľ�������ķ������Ȿ��Ĺؼ���ȷ����������꣮


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ��PC�С�O�ڵ�C��PA����O�ڵ�A��B��
��֪����ͼ��PC�С�O�ڵ�C��PA����O�ڵ�A��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��������ABC�ױ�BC��һ��P��PM��CA��AB��M����PN��BA��AC��N������P����MN�ĶԳƵ�P�䣮��֤��P����ڡ�ABC���Բ�ϣ���P��B��P��C=BP��PC��
��������ABC�ױ�BC��һ��P��PM��CA��AB��M����PN��BA��AC��N������P����MN�ĶԳƵ�P�䣮��֤��P����ڡ�ABC���Բ�ϣ���P��B��P��C=BP��PC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x2y-2x2y=x2y | B�� | 5y-3y=2 | C�� | -3x+5x=-8x | D�� | 3a+2b=5ab |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
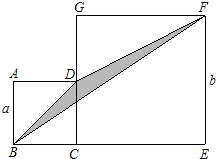 �ı���ABCD��CEFG���������Σ���������ABCD�ı߳�Ϊa��������CEFG�ı߳�Ϊb������BD��BF��DF��õ�������BDF�����ú���ĸa��b�Ĵ���ʽ��ʾ������BDF������ɱ�ʾΪ��������
�ı���ABCD��CEFG���������Σ���������ABCD�ı߳�Ϊa��������CEFG�ı߳�Ϊb������BD��BF��DF��õ�������BDF�����ú���ĸa��b�Ĵ���ʽ��ʾ������BDF������ɱ�ʾΪ��������| A�� | ab | B�� | $\frac{1}{2}$ab | C�� | $\frac{1}{2}$b2 | D�� | $\frac{1}{2}$a2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
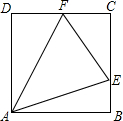 ��ͼ����֪������ABCD�ı߳�Ϊ1����E��F�ֱ��ڱ�BC��CD�ϣ��ҡ�EAF=45�㣬���CEF���ܳ�Ϊ2��
��ͼ����֪������ABCD�ı߳�Ϊ1����E��F�ֱ��ڱ�BC��CD�ϣ��ҡ�EAF=45�㣬���CEF���ܳ�Ϊ2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
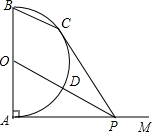 ��ͼ��AB�ǰ�ԲO��ֱ��������AM��AB����P��AM�ϣ�����OP����ԲO�ڵ�D��PC�а�ԲO�ڵ�C������BC��
��ͼ��AB�ǰ�ԲO��ֱ��������AM��AB����P��AM�ϣ�����OP����ԲO�ڵ�D��PC�а�ԲO�ڵ�C������BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
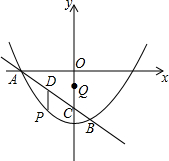 ��ͼ����֪������y=ax2+c��ֱ��$y=-\frac{3}{4}x-3$����A��B���㣬ֱ��AB��y�ύ�ڵ�C����B������Ϊ��1��$-\frac{15}{4}$��������P��ֱ��AB�·����������ϣ�����Q��y���ϣ�����D���߶�AB�ϣ���PD��y�ᣮ
��ͼ����֪������y=ax2+c��ֱ��$y=-\frac{3}{4}x-3$����A��B���㣬ֱ��AB��y�ύ�ڵ�C����B������Ϊ��1��$-\frac{15}{4}$��������P��ֱ��AB�·����������ϣ�����Q��y���ϣ�����D���߶�AB�ϣ���PD��y�ᣮ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
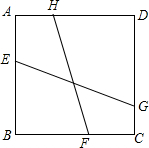 ��ͼ��������ABCD�У���E��F��G��H�ֱ����ڱ�AB��BC��CD��DA�ϣ���EG��FH�ļн�Ϊ45�㣬��������ABCD�ı߳���1��FH=$\frac{\sqrt{5}}{2}$����EG�ij�����$\frac{\sqrt{10}}{3}$��
��ͼ��������ABCD�У���E��F��G��H�ֱ����ڱ�AB��BC��CD��DA�ϣ���EG��FH�ļн�Ϊ45�㣬��������ABCD�ı߳���1��FH=$\frac{\sqrt{5}}{2}$����EG�ij�����$\frac{\sqrt{10}}{3}$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com