
【题目】定义:规定max(a,b)=![]() ,例如:max(﹣1,2)=2,max(3,3)=3.
,例如:max(﹣1,2)=2,max(3,3)=3.
感知:已知函数y=max(x+1,﹣2x+4)
(1)当x=3时,y=_____;
(2)当y=3时,x=______;
(3)当y随x的增大而增大时,x的取值范围为______;
(4)当﹣1≤x≤4时,y的取值范围为______;
探究:已知函数y=max(x+2,![]() )当直线y=m(m为常数)与函数y=max(x+2,
)当直线y=m(m为常数)与函数y=max(x+2,![]() )(﹣6<x≤3)的图象有两个公共点时,m的取值范围为_______;
)(﹣6<x≤3)的图象有两个公共点时,m的取值范围为_______;
拓展:已知函数y=max(﹣x2+2nx,﹣nx)(n为常数且n≠0),当![]() n﹣3≤x≤2时,随着x的增大,函数值y先减小后增大,直接写出n的取值范围.
n﹣3≤x≤2时,随着x的增大,函数值y先减小后增大,直接写出n的取值范围.
【答案】感知:(1)4;(2)2或![]() ;(3)x≥1;(4)2≤y≤6;探究:﹣2<m<﹣
;(3)x≥1;(4)2≤y≤6;探究:﹣2<m<﹣![]() 或4<m≤5;拓展:2≤n<6或n≤﹣6.
或4<m≤5;拓展:2≤n<6或n≤﹣6.
【解析】
感知:(1)利用题中新定义即可得到结果;
(2)利用题中新定义可对y=3所对应的的值进行分类得到两个方程,分别解方程即可求得结果;
(3)根据一次函数y=x+1和y=2x+4的图象特征,当y随x的增大而增大时,取函数y=x+1的图象部分,依题意可列出不等式,解不等式即可得出结果;
(4)根据题中新定义可列出y关于x的解析式,根据解析式和x的取值范围即可求得y的取值范围;
探究:同理(4)可得函数的解析式并画出图象,根据题意和图象即可求得m的取值范围;
拓展:先求出y=nx和y=﹣x2+2nx的图象交点,分n的情况可得函数的图象,再根据图象性质与题意列出不等式求解即可.
解:感知:(1)当x=3时,y=max(4,2),
∴y=4,
故答案为:4;
(2)当y=3时,
①当x+1=3,则x=2,此时y=max(3,0),
②当﹣2x+4=3,则x=![]() ,此时y=max(
,此时y=max(![]() ,3),
,3),
故答案为:2或![]() ;
;
(3)∵y随x的增大而增大,
∴y=x+1,
∴x+1≥﹣2x+4,
∴x≥1,
故答案为:x≥1;
(4)∵max(a,b)=![]() ,
,
当x+1<﹣2x+4时,y=﹣2x+4,此时x<1,
当x+1≥﹣2x+4时,y= x+1,此时x≥1,
∴y=![]() ,
,
∵﹣1≤x≤4,
当﹣1≤x<1时,y=﹣2x+4,此时2<y≤6,
当1≤x≤4时,y=x+1,此时2≤y≤5,
∴2≤y≤6,
故答案为:2≤y≤6;
探究:∵y=max(x+2,![]() )(﹣6<x≤3),
)(﹣6<x≤3),
同理(4)得:y= ,
,
如图所示,实线部分即为其图象,

由图象可得:当﹣6<x≤﹣4时,y=m与函数y=max(x+2,![]() )(﹣6<x≤3)的图象有两个公共点,则﹣2<m≤﹣
)(﹣6<x≤3)的图象有两个公共点,则﹣2<m≤﹣![]() ;
;
当0≤x≤3时,y=m与函数y=max(x+2,![]() )(﹣6<x≤3)的图象有两个公共点,4<m≤5;
)(﹣6<x≤3)的图象有两个公共点,4<m≤5;
综上所述:﹣2<m≤﹣![]() 或4<m≤5,
或4<m≤5,
故答案为:﹣2<m≤﹣![]() 或4<m≤5;
或4<m≤5;
拓展:y=﹣x2+2nx的对称轴为x=n,
令﹣x2+2nx=﹣nx,
解得:x=0或x=3n,
∴函数y=﹣x2+2nx与y=﹣nx的交点为(0,0)和(3n,3n2),
①当n≥2时,如图1,由图象可知:0≤x≤2时,函数y=﹣x2+2nx随x值的增大而增大,
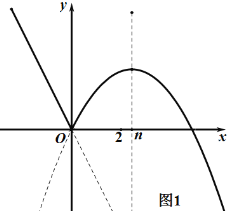
由题意得:![]() n3<0,
n3<0,
∴n<6,
∴2≤n<6;
②当n<0时,如图2,由图象可得:![]() n﹣3≥n,
n﹣3≥n,
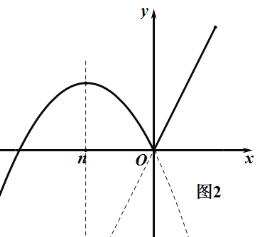
∴n≤﹣6;
综上所述:2≤n<6或n≤﹣6.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
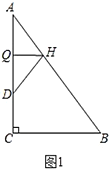
(1)如图1,折叠![]() 使点
使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕交
处,折痕交![]() 、
、![]() 分别于点
分别于点![]() 、
、![]() ,若
,若![]() ,则
,则![]() ________.
________.
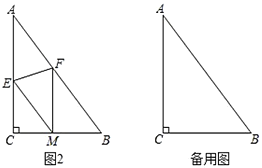
(2)如图2,折叠![]() 使点
使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕交
处,折痕交![]() 、
、![]() 分别于点
分别于点![]() 、
、![]() .若
.若![]() ,求证:四边形
,求证:四边形![]() 是菱形;
是菱形;
(3)在(1)(2)的条件下,线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 和
和![]() 相似?若存在,求出
相似?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
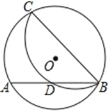
【题目】如图,在⊙O 中,点 C 在优弧 AB 上,将弧 BC 沿直线 BC 折叠后刚好经过弦 AB 的 中点 D.若⊙O 的半径为![]() ,AB=4,则 BC 的长是( )
,AB=4,则 BC 的长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解密数学魔术:魔术师请观众心想一个数,然后将这个数按以下步骤操作:
![]()
魔术师能立刻说出观众想的那个数.
(1)如果小玲想的数是![]() ,请你通过计算帮助她告诉魔术师的结果;
,请你通过计算帮助她告诉魔术师的结果;
(2)如果小明想了一个数计算后,告诉魔术师结果为85,那么魔术师立刻说出小明想的那个数是:__________;
(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数.若设观众心想的数为![]() ,请你按照魔术师要求的运算过程列代数式并化简,再用一句话说出这个魔术的奥妙.
,请你按照魔术师要求的运算过程列代数式并化简,再用一句话说出这个魔术的奥妙.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是长春新地标一一摩天活力城楼顶上的摩天轮,被誉为“长春眼”,如图②是其正面的平面图.已知摩天活力城楼顶AD距地面BC为34米,摩天轮⊙O与楼顶AD近似相切,切点为G.测得∠OEF=∠OFE=67°,EF=27.54米,求摩天轮的最高点到地面BC的距离.(结果精确到0.1米)(参考数据:sin67°=0.92,cos67°0.39,tan67°=2.36)
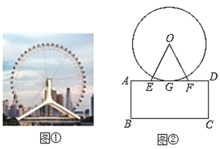
查看答案和解析>>
科目:初中数学 来源: 题型:
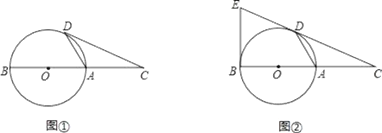
【题目】已知点C为直径BA的延长线上一点,CD切⊙O于点D,
(Ⅰ)如图①,若∠CDA=26°,求∠DAB的度数;
(Ⅱ)如图②,过点B作⊙O的切线交CD的延长线于点E,若⊙O的半径为3,BC=10,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防新冠肺炎,某药店销售甲、乙两种防护口罩,已知甲口罩每袋的售价比乙口罩多5元,小明从该药店购买了3袋甲口罩和2袋乙口罩共花费115元.
(1)求该药店甲、乙两种口罩每袋的售价分别为多少元?
(2)根据消费者需求,药店决定用不超过8000元购进甲、乙两种口罩共400袋.已知甲口罩每袋的进价为22.2元,乙口罩每袋的进价为17.8元,要使药店获利最大,应该购进甲、乙两种口罩各多少袋,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
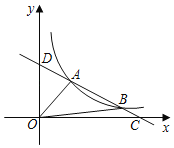
【题目】如图,点A(m,3)、B(6,n)在双曲线y=![]() (x>0)上,直线y=ax+b经过A、B两点,并与x轴、y轴分别相交手C、D两点,已知S△OAB=8.
(x>0)上,直线y=ax+b经过A、B两点,并与x轴、y轴分别相交手C、D两点,已知S△OAB=8.
(1)求双曲线y=![]() 的函数表达式;
的函数表达式;
(2)求△COD的周长;
(3)直接写出不等式![]() -ax>b的解集.
-ax>b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(﹣1,1),点B在x轴正半轴上,点D在第三象限的双曲线y=![]() 上,过点C作CE∥x轴交双曲线于点E,则CE的长为( )
上,过点C作CE∥x轴交双曲线于点E,则CE的长为( )

A. ![]() B.
B. ![]() C. 3.5D. 5
C. 3.5D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com