
 如图,在平面直角坐标系中,?OABC的边OA在x轴上,∠COA=30°,OC=8,AC⊥OA,对角线OB与AC相较于点M,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C.
如图,在平面直角坐标系中,?OABC的边OA在x轴上,∠COA=30°,OC=8,AC⊥OA,对角线OB与AC相较于点M,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C.分析 (1)先解Rt△OAC,得出CA=4,OA=4$\sqrt{3}$,那么C(4$\sqrt{3}$,4),再将C点坐标代入反比例函数解析式,即可求解;
(2)先根据平行四边形的对角线互相平分得出AM=$\frac{1}{2}$AC=2.设平移的距离为d,根据平移的性质求出平移后的点M的坐标为(4$\sqrt{3}$+d,2),再根据此时点M在反比例函数的图象上得出(4$\sqrt{3}$+d)×2=16$\sqrt{3}$,解方程即可.
解答 解:(1)在Rt△OAC中,∠COA=30°,OC=8,
∴CA=4,OA=4$\sqrt{3}$,
∴C(4$\sqrt{3}$,4),
∴k=4$\sqrt{3}$×4=16$\sqrt{3}$,
∴反比例函数的表达式为y=$\frac{16\sqrt{3}}{x}$(x>0);
(2)∵点M是?OABC两对角线的交点,
∴AM=$\frac{1}{2}$AC=2.
设平移的距离为d,则平移后的点M的坐标为(4$\sqrt{3}$+d,2),
∴(4$\sqrt{3}$+d)×2=16$\sqrt{3}$,
解得d=4$\sqrt{3}$.
故平移的距离为4$\sqrt{3}$个单位长度.
点评 本题考查了待定系数法求反比例函数解析式,平行四边形的性质,平移的性质,反比例函数图象上点的坐标特征,难度适中.正确求出解析式是解题的关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图.
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD与正方形AEFG起始时互相重合,现将正方形AEFG绕点A逆时针旋转,设旋转角∠BAE=α(0°<α<360°),则当正方形的顶点F落在正方形的对角线AC或BD所在直线上时,α=60°或180°或300°.
如图,正方形ABCD与正方形AEFG起始时互相重合,现将正方形AEFG绕点A逆时针旋转,设旋转角∠BAE=α(0°<α<360°),则当正方形的顶点F落在正方形的对角线AC或BD所在直线上时,α=60°或180°或300°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,点A(0,m+4),点C(5m+3,0)在x轴的正半轴上,现将点C向左平移4单位长度再向上平移7个单位长度得到对应点B(7m-7,n).
如图,在平面直角坐标系xOy中,点A(0,m+4),点C(5m+3,0)在x轴的正半轴上,现将点C向左平移4单位长度再向上平移7个单位长度得到对应点B(7m-7,n).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
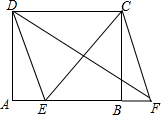 在矩形ABCD中,AD=3,AB=4,点E在线段AB上,将AE平移至BF.
在矩形ABCD中,AD=3,AB=4,点E在线段AB上,将AE平移至BF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 时钟摆动的钟摆 | B. | 在笔直的公路上行驶的汽车 | ||
| C. | 随风摆动的旗帜 | D. | 汽车玻璃窗上两刷的运动 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知三角形ABC中,∠A=56°,∠ABC=90°,AB=8cm,BC=12cm,现将三角形ABC沿直线CB向左平移xcm(x<12,且x是正数),得到新的三角形DEF,DF交AB与点G.
如图,已知三角形ABC中,∠A=56°,∠ABC=90°,AB=8cm,BC=12cm,现将三角形ABC沿直线CB向左平移xcm(x<12,且x是正数),得到新的三角形DEF,DF交AB与点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△ABC和△A1B1C1关于点E成中心对称.
如图,在平面直角坐标系中,△ABC和△A1B1C1关于点E成中心对称.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com