
 如图,在△ABC中,D,E分别是AB,BC边上的点,且DE∥AC,若S△BDE:S△DEC=1:3,则S△BDE:S四边形ACED的值为( )
如图,在△ABC中,D,E分别是AB,BC边上的点,且DE∥AC,若S△BDE:S△DEC=1:3,则S△BDE:S四边形ACED的值为( )| A. | 1:9 | B. | 1:12 | C. | 1:15 | D. | 1:16 |
科目:初中数学 来源: 题型:解答题
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 70 | 128 | 171 | 302 | 481 | 599 | 903 |
| 摸到白球的频率 $\frac{m}{n}$ | 0.75 | 0.64 | 0.57 | 0.604 | 0.601 | 0.599 | 0.602 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC,CE⊥AD交AB于点E,BE=CF,BF交CE于点P,连接PD,下列结论:①AC=AE;②CD=BE;③PB=PF;④DP⊥BF,其中正确的结论是( )
如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC,CE⊥AD交AB于点E,BE=CF,BF交CE于点P,连接PD,下列结论:①AC=AE;②CD=BE;③PB=PF;④DP⊥BF,其中正确的结论是( )| A. | ①②③④ | B. | ①②③ | C. | ①② | D. | ①③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
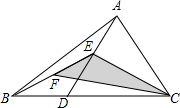 如图,在△ABC中,点D是BC边上的任意一点,E是AD中点,F是BE中点,连结CE,CF,若点D从点B运动到点C,则△CEF的面积( )
如图,在△ABC中,点D是BC边上的任意一点,E是AD中点,F是BE中点,连结CE,CF,若点D从点B运动到点C,则△CEF的面积( )| A. | 一直变大 | B. | 一直变小 | C. | 先变大再变小 | D. | 不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$cm | B. | 4$\sqrt{2}$cm | C. | 2$\sqrt{6}$cm | D. | 2$\sqrt{5}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 二次函数y=ax2+bx+c的图象如图所示,P(n,2)是图象上的一点,且AP⊥BP,则a=( )
二次函数y=ax2+bx+c的图象如图所示,P(n,2)是图象上的一点,且AP⊥BP,则a=( )| A. | -2 | B. | -3 | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{3}{4}$ | C. | 4 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com