
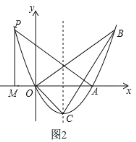
【题目】如图,已知抛物线经过点![]() ,
,![]() 及原点
及原点![]() ,顶点为
,顶点为![]() .
.

(1)求抛物线的解析式:
(2)试判断![]() 的形式,并说明理由:
的形式,并说明理由:
(3)![]() 是抛物线上第二象限内的动点,过点
是抛物线上第二象限内的动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,是否存在点
,是否存在点![]() 使得以点
使得以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出点
相似?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】![]()
![]() ;
;![]() 是直角三角形
是直角三角形![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]()
【解析】
(1)根据抛物线过A(2,0)及原点可设y=a(x-2)x,然后根据抛物线y=a(x-2)x过B(3,3),求出a的值即可;
(2)利用两点间距离公式OB2=18,OC2=2,BC2=20,利用勾股定理逆定理即可得出结论.
(3)分△PMA∽△COB和△PMA∽△BOC表示出PM和AM,从而表示出点P的坐标,代入求得的抛物线的解析式即可求得t的值,从而确定点P的坐标.
![]() 根据抛物线过
根据抛物线过![]() 及原点,可设
及原点,可设![]() ,
,
又∵抛物线![]() 过
过![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴抛物线的解析式为![]() ;
;![]() 由
由![]() 知抛物线解析式为
知抛物线解析式为![]() ;
;
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 是直角三角形.
是直角三角形.![]() 由
由![]() 知,
知,![]() 为直角三角形,
为直角三角形,![]() ,且
,且![]() ,
,
①如图![]() ,
,

若![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∴点![]() ,
,
代入![]() 得
得![]() ,
,
解得![]() (舍)或
(舍)或![]() ,
,
∴![]() 的坐标为
的坐标为![]() ;
;
②如图![]() ,
,
若![]() ,
,
∴![]()
设![]() ,则
,则![]() ,
,
点![]() ,代入
,代入![]() 得
得![]() ,
,
解得![]() (舍),
(舍),![]() ,
,
∴![]()
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如图所示,在ΔABC和ΔADE中,AB=AC,AD=AE,∠BAC=∠DAE,,且点B,A,D在同一条直线上,连接BE,CD,M,N分别为BE,CD的中点, 连接AM,AN,MN.
⑴.求证:BE=CD
⑵.求证:ΔAMN是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
(1)求证:AB=AD;
(2)求证:CD平分∠ACE.
(3)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,则该函数图象的开口________(填“向上”或“向下”);若点
,则该函数图象的开口________(填“向上”或“向下”);若点![]() 在该二次函数的图象上,则点
在该二次函数的图象上,则点![]() 在第二象限内为________(填“随机”“必然”或“不可能”)事件.
在第二象限内为________(填“随机”“必然”或“不可能”)事件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一间房子的两墙之间有一个底端在![]() 点的梯子,当它靠在一侧墙上时,梯子的顶端在
点的梯子,当它靠在一侧墙上时,梯子的顶端在![]() 点;当它靠在另一侧墙上时梯子的顶端在
点;当它靠在另一侧墙上时梯子的顶端在![]() 点.已知
点.已知![]() ,
,![]() ,点
,点![]() 到地面的垂直距离为
到地面的垂直距离为![]() 米,则点
米,则点![]() 到地面的垂直距离约是________米(精确到
到地面的垂直距离约是________米(精确到![]() ).
).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com