
如图,直线y=-2x+2与x轴、y轴分别交于A、B两点,将△OAB绕点O逆时针方向旋转90°后得到△OCD.
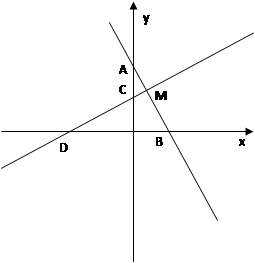
(1)填空:点C的坐标是( , ),点D的坐标是( , );
(2)设直线CD与AB交于点M,求线段BM的长;
(3)在y轴上是否存在点P,使得△BMP是等腰三角形?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.
(1)点C的坐标是(0,1),点D的坐标是(-2,0),(2)BM=,(3)存在
解析:因为△OAB绕点O逆时针方向旋转90°后得到△OCD,所以OB=OC=1,OA=OD=2所以点C的坐标是(0,1),点D的坐标是(-2,0) ……………… 2分
(2)方法一:由(1)可知CD= =,BC=1
又∠1=∠5,∠4=∠3
∴△BMC∽△DOC ………………2分
∴= 即=
∴BM= ………………2分
方法二:设直线CD的解析式为y=kx+b
由(1)得
解得
∴直线CD的解析式为y= x+1
又∠1=∠5,∠BCM=∠DCO
∴△BMC∽△DOC ………………2分
∴= 即=
∴BM= ………………2分
方法三
∵ ∴
∴M的坐标为(,) ………………2分
过点M作ME⊥y轴于点E,则ME=,BE=
∴BM= = ………………2分
(3)存在
分两种情况讨论:
① 以BM为腰时
∵BM=,又点P在y轴上,且BP=BM
时满足条件的点P有两个,它们是P1 (0,2+)、P2 (0,2-)…………2分
过点M作ME⊥y轴于点E,∵∠BMC=90°,
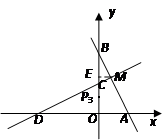
 则△BME∽△BCM
则△BME∽△BCM
∴=
∴BE==
又∵BM=BP
∴PE=BE=
∴BP=
∴OP=2-=
此时满足条件的点P有一个,它是P3 (0,) ……………1分
② 以BM为底时,作BM的垂直平分线,分别交y轴、BM于点P、F,
 由(2)得∠BMC=90°,
由(2)得∠BMC=90°,
∴PF∥CM
∵F是BM的中点,
∴BP=BC=
∴OP=
此时满足条件的点P有一个,它是P4 (0,) ……………… 1分
综上所述点P有四个:P1 (0,2+)、P2 (0,2-)、P3 (0,) P4 (0,)


科目:初中数学 来源: 题型:
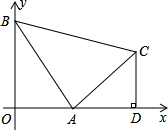 腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D.
腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:
| 8 | x |
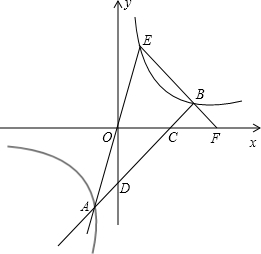 轴分别交于点C、D.直线EB交x轴于点F.
轴分别交于点C、D.直线EB交x轴于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
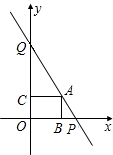 如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.
如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com