
【题目】在我市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图. 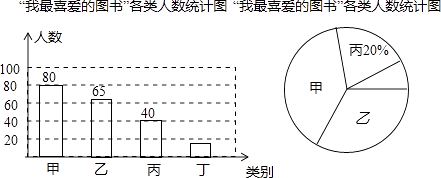
请你结合图中信息,解答下列问题:
(1)本次共调查了名学生;
(2)被调查的学生中,最喜爱丁类图书的有人,最喜爱甲类图书的人数占本次被调查人数的%;
(3)在最喜爱丙类学生的图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生1500人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人.
【答案】
(1)200
(2)15;40
(3)解:设男生人数为x人,则女生人数为1.5x人,由题意得:
x+1.5x=1500×20%,
解得:x=120,
当x=120时,1.5x=180.
答:该校最喜爱丙类图书的女生和男生分别有180人,120人
【解析】解:(1)共调查的学生数: 40÷20%=200(人);
故答案为:50;
⑵最喜爱丁类图书的学生数:200﹣80﹣65﹣40=15(人);
最喜爱甲类图书的人数所占百分比:80÷200×100%=40%;
故答案为:15,40;
(1)根据百分比=频数÷总数可得共调查的学生数;(2)最喜爱丁类图书的学生数=总数减去喜欢甲、乙、丙三类图书的人数即可;再根据百分比=频数÷总数计算可得最喜爱甲类图书的人数所占百分比;(3)设男生人数为x人,则女生人数为1.5x人,由题意得方程x+1.5x=1500×20%,解出x的值可得答案.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知l1∥l2,直线l1经过原点O,直线l2对应的函数表达式为![]() ,点A在直线l2上,AB⊥l1,垂足为B,则线段AB的长为( )
,点A在直线l2上,AB⊥l1,垂足为B,则线段AB的长为( )
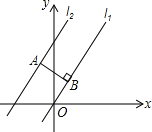
A. 4 B. 6 C. 8 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④AD平分∠CDE;⑤S△ABD:S△ACD=AB:AC,其中正确的有( )
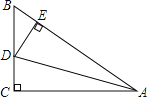
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,4),B(-4,1),C(-1,2).
(1)在图中作出△ABC关于x轴的对称图形△A1B1C1;
(2)请直接写出点C关于y轴的对称点C'的坐标: ;
(3)△ABC的面积= ;
(4)在y轴上找一点P,使得△PAC周长最小,并求出△PAC周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线l1:y=2x+1
(1)若将直线l1平移,使之经过点(1,-5),求平移后直线的解析式;
(2)若直线l2:y=x+m与直线l1的交点在第二象限,求m的取值范围;
(3)如图,直线y=x+b与直线y=nx+2n(n≠0)的交点的横坐标为-5,求关于x的不等式组0<nx+2n<x+b的解集.
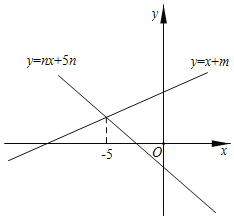
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学初三年级300名男学生的身体发育情况,从中对20名男学生的身高进行了测量,结果如下:(单位:cm)
175 161 171 176 167 181 161 173 171 177
179 172 165 157 173 173 166 177 169 181
下表是根据上述数据填写的表格的一部分:
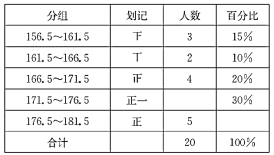
(1)请填写表中未完成的部分;
(2)该校初三年级男学生身高在171.5~176.5(cm)范围内的人数为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+ ![]() .其中正确的个数为( )
.其中正确的个数为( ) 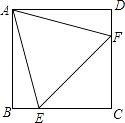
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图, ![]() 是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是
是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是![]() ,当点P到达点B时,P、Q两点停止运动,设点P的运动时间
,当点P到达点B时,P、Q两点停止运动,设点P的运动时间![]() ,解答下列各问题:
,解答下列各问题:
![]() 经过
经过![]() 秒时,求
秒时,求![]() 的面积;
的面积;
![]() 当t为何值时,
当t为何值时, ![]() 是直角三角形?
是直角三角形?
![]() 是否存在某一时刻t,使四边形APQC的面积是
是否存在某一时刻t,使四边形APQC的面积是![]() 面积的三分之二?如果存在,求出t的值;不存在请说明理由.
面积的三分之二?如果存在,求出t的值;不存在请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com