
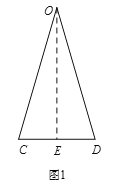
【题目】如图所示的是常见的工具“人字梯”,量得“人字梯”的一侧OC=OD=2.5米,
(1)若CD=1.4米,求梯子顶端O离地面的高度;

(2)《建筑施工高处作业安全技术规范》规定:使用“人字梯”时,上部夹角(∠AOB)以35°~45°为宜,铰链必须牢固,并应有可靠的拉撑措施.如图,小明在人字梯的一侧A、B处系上一根绳子确保用梯安全,他测得OA=OB=2米,在A、B处打结各需要0.4米的绳子,请你帮小明计算一下,他需要的绳子的长度应该在什么范围内.(结果精确到0.1米,参考数据:sin17.5°≈0.30,cos17.5°≈0.95,tan17. °5≈0.32,sin22.5°≈0.38,cos22.5°≈0.92,tan22.5°≈0.41)
【答案】(1) 2.4米; (2)他所需的绳子的长度应该在2.0米到2.3米之间.
【解析】分析:画出与实际问题对应的图形,(1)作OE⊥CD于点E,用勾股定理求OE;(2)作OF⊥AB于点F,分别求出当∠AOE=35°和45°时的AB的长.
详解:(1)如图1,作OE⊥CD于点E,
△OCD中,∵OC=OD,且OE⊥CD.CE=![]() CD=0.7,
CD=0.7,
所以OE=![]() =2.4米;
=2.4米;
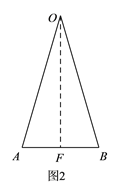
(2)如图2,作OF⊥AB于点F,
△OAB中,OA=OB,且OF⊥AB,
所以∠AOF=∠BOF=![]() ∠AOB,AF=FB=
∠AOB,AF=FB=![]() AB.
AB.
Rt△OAF中,sin∠AOF=![]() ,
,
∴AF=OA·sin∠AOF,
由题意知35°≤∠AOB≤45°,
当∠AOF=17.5°时,AF=OA·sin∠AOF=2×sin17.5°≈0.60米,
此时,AB≈1.20米,所需的绳子约为2.0米,
当∠AOF=22.5°时,AF=OA·sin∠AOF=2×sin22.5°≈0.76米,
此时,AB≈1.52米,所需的绳子约为2.3米,
所以,他所需的绳子的长度应该在2.0米到2.3米之间.


科目:初中数学 来源: 题型:
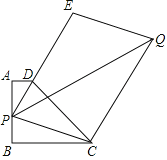
【题目】已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=3,BC=4.若P为线段AB上任意一点,延长PD到E,使DE=2PD,再以PE、PC为边作平行四边形PCQE,求对角线PQ的最小值为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当DE=AE时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.其中正确的是( )

A.②③B.②④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师计划组织朋友去晋西北游览两日,经了解,现有甲、乙两家旅行社比较合适,报价均为每人![]() 元,且提供的服务完全相同.针对组团两日游的游客,甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过
元,且提供的服务完全相同.针对组团两日游的游客,甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过![]() 人,每人都按九折收费,若超过
人,每人都按九折收费,若超过![]() 人,则其中
人,则其中![]() 人按九折收费,超出人数每人按七五折收费.假设组团参加两日游的人数为
人按九折收费,超出人数每人按七五折收费.假设组团参加两日游的人数为![]() 人.
人.
(1)请分别列式表示甲、乙两家旅行社收取组团两日游的总费用;
(2)若王老师组团参加两日游的人数共有![]() 人,请你通过计算,在甲、乙两家旅行社中,帮助王老师选择收取总费用较少的一家.
人,请你通过计算,在甲、乙两家旅行社中,帮助王老师选择收取总费用较少的一家.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,已知AB=6,BC=9, ![]() .对角线AC、BD交于点O.动点P在边AB上,⊙P经过点B,交线段PA于点E.设BP= x.
.对角线AC、BD交于点O.动点P在边AB上,⊙P经过点B,交线段PA于点E.设BP= x.
(1)求AC的长;
(2)设⊙O的半径为y,当⊙P与⊙O外切时,求y关于x的函数解析式,并写出定义域;
(3)如果AC是⊙O的直径,⊙O经过点E,求⊙O与⊙P的圆心距OP的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个有50个奇数排成的数阵,用如图所示的框去框住四个数,并求出这四个数的和,在下列给出的备选答案中,有可能是这四个数的和的是( )

A. 114 B. 122 C. 220 D. 84
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品每天的利润为y元。
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?最大利润是多少?
(3)该商品在销售过程中,共有多少天每天的销售利润不低于4800元?请直接写出结果。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车运输公司根据实际需要计划购买大、中型两种客车共20辆,已知大型客车每辆62万元,中型客车每辆40万元,设购买大型客车x(辆),购车总费用为y(万元).
(1)求y与x的函数关系式(不要求写出自变量x的取值范围);
(2)若购买中型客车的数量少于大型客车的数量,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com