
 如图,四边形ABCD,对角线AC与BD相交于O,下列4个命题:
如图,四边形ABCD,对角线AC与BD相交于O,下列4个命题:分析 根据对角线互相垂直的四边形的面积等于对角线乘积的一半可得(1)正确;根据两直线平行,内错角相等可得∠OAD=∠OCB,再利用“角边角”证明△AOD和△COB全等,根据全等三角形对应边相等可得OB=OD,然后根据对角线互相平分的四边形是平行四边形判断出四边形ABCD是平行四边形,从而判断出(2)正确;若根据相似三角形对应角相等可得∠OAD=∠OBC,然后判断出点A、B、C、D四点共圆,再根据同弧所对的圆周角相等可得∠BAC=∠BDC;若根据相似三角形对应角相等可得∠OAD=∠OCB,再根据内错角相等,两直线平行可得AD∥BC,无法确定出∠BAC=∠BDC,判断出(3)错误;先判断出点A、B、C、D四点共圆,然后根据同弧所对的圆周角相等可得∠OAD=∠OBC,∠ODA=∠OCB,然后判断出△OAD与△BOC相似,从而得到(4)正确.
解答 解:(1)∵AC⊥BD,
∴S四边形ABCD=$\frac{1}{2}$AC•BD,故本小题正确;
(2)∵AD∥BC,
∴∠OAD=∠OCB,
在△AOD和△COB中,
$\left\{\begin{array}{l}{∠OAD=∠OCB}\\{AO=CO}\\{∠AOD=∠COB}\end{array}\right.$,
∴△AOD≌△COB(ASA),
∴OB=OD,
又∵AO=CO,
∴四边形ABCD是平行四边形,故本小题正确;
(3)①由△OAD与△BOC相似得,∠OAD=∠OBC,
所以,点A、B、C、D四点共圆,
所以,∠BAC=∠BDC,此时本题结论正确;
②由△OAD与△BOC相似得,∠OAD=∠OCB,
所以,AD∥BC,
此时若点A、B、C固定,则∠BAC大小不变,∠BDC随点D的左右移动而变化,
所以,无法确定出∠BAC=∠BDC,
综上所述,△OAD与△BOC相似,无法确定出∠BAC=∠BDC,故本小题错误;
(4)∵∠BAC=∠BDC,
∴点A、B、C、D四点共圆,
∴∠OAD=∠OBC,∠ODA=∠OCB,
∴△OAD与△BOC相似,故本小题正确;
综上所述,真命题是(1)(2)(4).
故答案为:(1)(2)(4).
点评 本题考查了命题与定理,主要利用了对角线互相垂直的四边形的面积的求法,全等三角形的判定与性质,相似三角形的判定与性质,四点共圆的知识,综合题,难度较大,(3)(4)考虑利用四点共圆求解是解题的关键.


科目:初中数学 来源: 题型:填空题
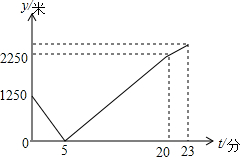 小明在上学的路上(假定从家到校只有这一条路)发现忘带眼镜,立刻停下,往家里打电话,妈妈接到电话后立刻带上眼镜赶往学校.同时,小明原路返回,两人相遇后小明立即赶往学校,妈妈回家,妈妈要15分钟到家,小明再经过3分钟到校.小明始终以100米/分的速度步行,小明和妈妈之间的距离y(米)与小明打完电话后的步行时间t(分)之间函数图象如图所示,则下列结论:①打电话时,小明与妈妈的距离为1250米;②打完电话后,经过23分钟小明到达学校;③小明与妈妈相遇后,妈妈回家的速度为150米/分;④小明家与学校的距离为2550米.其中正确的有①②④.(把正确的序号都填上)
小明在上学的路上(假定从家到校只有这一条路)发现忘带眼镜,立刻停下,往家里打电话,妈妈接到电话后立刻带上眼镜赶往学校.同时,小明原路返回,两人相遇后小明立即赶往学校,妈妈回家,妈妈要15分钟到家,小明再经过3分钟到校.小明始终以100米/分的速度步行,小明和妈妈之间的距离y(米)与小明打完电话后的步行时间t(分)之间函数图象如图所示,则下列结论:①打电话时,小明与妈妈的距离为1250米;②打完电话后,经过23分钟小明到达学校;③小明与妈妈相遇后,妈妈回家的速度为150米/分;④小明家与学校的距离为2550米.其中正确的有①②④.(把正确的序号都填上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com