
分析 (1)首先化简二次根式进而合并求出答案;
(2)首先乘法公式以及二次根式乘法化简进而合并求出答案.
解答 解:(1)$\sqrt{12}$-9$\sqrt{\frac{1}{3}}$+$\sqrt{75}$
=2$\sqrt{3}$-9×$\frac{\sqrt{3}}{3}$+5$\sqrt{3}$
=2$\sqrt{3}$-3$\sqrt{3}$+5$\sqrt{3}$
=4$\sqrt{3}$;
(2)($\sqrt{2}$-$\sqrt{3}$)2+2$\sqrt{\frac{1}{3}}$×3$\sqrt{2}$
=2+3-2$\sqrt{6}$+6$\sqrt{\frac{2}{3}}$
=5-2$\sqrt{6}$+6×$\frac{\sqrt{6}}{3}$
=5.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
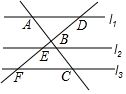 如图,已知l1∥l2∥l3,直线AC、DF分别交直线l1、l2、l3于点A、B、C,和点D、E、F,若DE=2,DF=3,则下列结论中,错误的是( )
如图,已知l1∥l2∥l3,直线AC、DF分别交直线l1、l2、l3于点A、B、C,和点D、E、F,若DE=2,DF=3,则下列结论中,错误的是( )| A. | $\frac{AD}{CF}$=$\frac{2}{3}$ | B. | $\frac{BC}{AB}$=$\frac{1}{2}$ | C. | $\frac{AB}{AC}$=$\frac{2}{3}$ | D. | $\frac{EF}{DF}$=$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | n2-1 | B. | 12+22+32+…+i2-i | ||
| C. | 12+22+32+…+n2-1 | D. | 12+22+32+…+n2-(1+2+3+…+n ) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
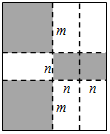 如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为m厘米的大正方形,两块是边长都为n厘米的小正方形,五块是长宽分别是m厘米、n厘米的全等小矩形,且m>n.
如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为m厘米的大正方形,两块是边长都为n厘米的小正方形,五块是长宽分别是m厘米、n厘米的全等小矩形,且m>n.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
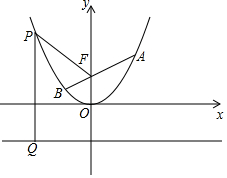 已知抛物线C:y=$\frac{1}{4}$x2+bx+c在x=1和x=-1时的函数值相等,且x=2时y=1,P(x,y)为抛物线C上任一点,F(0,1)为y轴上一点,PQ与直线y=-1垂直交于点Q
已知抛物线C:y=$\frac{1}{4}$x2+bx+c在x=1和x=-1时的函数值相等,且x=2时y=1,P(x,y)为抛物线C上任一点,F(0,1)为y轴上一点,PQ与直线y=-1垂直交于点Q查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com